已知{an}是等差数列,其前n项和为Sn,{bn}是等比数列,且a1=b1=2,a4+b4=27,s4-b4=10.
(1)求数列{an}与{bn}的通项公式;
(2)记Tn=anb1+an-1b2+…+a1bn,n∈N*,证明:Tn+12=-2an+10bn(n∈N*).
【答案】
分析:(1)直接设出首项和公差,根据条件求出首项和公差,即可求出通项.
(2)先写出T
n的表达式;方法一:借助于错位相减求和;
方法二:用数学归纳法证明其成立.
解答:解:(1)设等差数列的公差为d,等比数列的公比为q,
由a
1=b
1=2,得a
4=2+3d,b
4=2q
3,s
4=8+6d,
由条件a
4+b
4=27,s
4-b
4=10,
得方程组
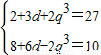
,解得
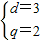
,
故a
n=3n-1,b
n=2
n,n∈N
*.
(2)证明:方法一,由(1)得,T
n=2a
n+2
2a
n-1+2
3a
n-2+…+2
na
1; ①;
2T
n=2
2a
n+2
3a
n-1+…+2
na
2+2
n+1a
1; ②;
由②-①得,T
n=-2(3n-1)+3×2
2+3×2
3+…+3×2
n+2
n+2=
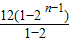
+2
n+2-6n+2
=10×2
n-6n-10;
而-2a
n+10b
n-12=-2(3n-1)+10×2
n-12=10×2
n-6n-10;
故T
n+12=-2a
n+10b
n(n∈N
*).
方法二:数学归纳法,
③当n=1时,T
1+12=a
1b
1+12=16,-2a
1+10b
1=16,故等式成立,
④假设当n=k时等式成立,即T
k+12=-2a
k+10b
k,
则当n=k+1时有,
T
k+1=a
k+1b
1+a
kb
2+a
k-1b
3+…+a
1b
k+1=a
k+1b
1+q(a
kb
1+a
k-1b
2+…+a
1b
k)
=a
k+1b
1+qT
k=a
k+1b
1+q(-2a
k+10b
k-12)
=2a
k+1-4(a
k+1-3)+10b
k+1-24
=-2a
k+1+10b
k+1-12.
即T
k+1+12=-2a
k+1+10b
k+1,因此n=k+1时等式成立.
③④对任意的n∈N
*,T
n+12=-2a
n+10b
n成立.
点评:本题主要考察等差数列和等比数列的综合问题.解决这类问题的关键在于熟练掌握基础知识,基本方法.并考察计算能力.

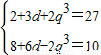 ,解得
,解得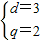 ,
,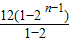 +2n+2-6n+2
+2n+2-6n+2

 名校课堂系列答案
名校课堂系列答案 满足:
满足: .
.