
(1)y=sin(3x-![]() );(2)y=cos(-2x+
);(2)y=cos(-2x+![]() ).
).
解:(1)令3x-![]() =u,y=sinu的单调增区间为[2kπ-
=u,y=sinu的单调增区间为[2kπ-![]() ,2kπ+
,2kπ+![]() ],(k∈Z).
],(k∈Z).
即2kπ-![]() ≤3x-
≤3x-![]() ≤2kπ+
≤2kπ+![]() .
.
∴原函数单调增区间为[![]() ](k∈Z).
](k∈Z).
又y=sinu的单调减区间为[2kπ+![]() ,2kπ+
,2kπ+![]() ],(k∈Z),
],(k∈Z),
即2kπ+![]() ≤3x-
≤3x-![]() ≤2kπ+
≤2kπ+![]() ,
,
∴原函数的单调减区间为
[![]() ](k∈Z).
](k∈Z).
(2)∵y=cos(-2x+![]() )=cos(2x-
)=cos(2x-![]() ),令2x-
),令2x-![]() =u,y=cosu的单调增区间为[2kπ-π,2kπ],(k∈Z)即2kπ-π≤2x-
=u,y=cosu的单调增区间为[2kπ-π,2kπ],(k∈Z)即2kπ-π≤2x-![]() ≤2kπ,
≤2kπ,
解得:kπ-![]() ≤x≤kπ+
≤x≤kπ+![]() (k∈Z).
(k∈Z).
∴原函数的增区间为:[kπ-![]() ,kπ+
,kπ+![]() ],k∈Z.
],k∈Z.
∵y=cosu的单调减区间为[2kπ,2kπ+π],k∈Z.
即:2kπ≤2x-![]() ≤2kπ+π,解得:kπ+
≤2kπ+π,解得:kπ+![]() ≤x≤kπ+
≤x≤kπ+![]() ,k∈Z.
,k∈Z.
∴原函数的减区间为[kπ+![]() ,kπ+
,kπ+![]() ],k∈Z.
],k∈Z.


科目:高中数学 来源:2012年人教A版高中数学必修四1.4三角函数的图像与性质练习卷(四)(解析版) 题型:解答题
求下列函数的单调区间:
(1)y=tan ; (2)y=
; (2)y= tan2x+1;
tan2x+1;
(3)y=3tan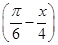 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com