练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    方程＝l(k＞0)有且仅有两个不同的实数解，φ(＞φ)，则以下有关两根关系的结论正确的是

    [　　]
    A．

    sinφ＝φcos

    B．

    sinφ＝－φcos

    C．

    cosφ＝sin

    D．

    sin＝－sinφ

    答案：B
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：高考零距离　二轮冲刺优化讲练　数学 题型：044

    如图所示，已知双曲线S的两条渐近线过坐标原点，且与以点A(，0)为圆心、1为半径的圆相切，双曲线S的一个顶点与点A关于直线y＝x对称．设直线l过点A，斜率为k．

    (1)

    求双曲线S的方程

    (2)

    当k＝1时，在双曲线S的上支上求点B，使其与直线l的距离为

    (3)

    当0≤k＜1时，若双曲线S的上支上有且只有一个点B到直线l的距离为，求斜率k的值及相应的点B的坐标．

    查看答案和解析>>

    科目：高中数学 来源：湖南省长沙市雅礼中学2009届高三第六次月考数学理试卷 题型：044

    已知A(1，0)，B(－2，0)，动点M满足∠MBA＝2∠MAB(∠MAB≠0)．

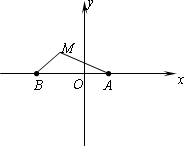
    (1)求动点M的轨迹E的方程；

    (2)若直线l：y＝k(x＋7)，且轨迹E上存在不同两点C．D关于直线l对称．

    ①求直线l斜率k的取值范围；

    ②是否可能有A、B、C、D四点共圆？若可能，求实数k取值的集合；若不可能，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2012年普通高等学校招生全国统一考试山东卷数学理科 题型：044

    在平面直角坐标系xOy中，F是抛物线C：x2＝2py(p＞0)的焦点，M是抛物线C上位于第一象限内的任意一点，过M，F，O三点的圆的圆心为Q，点Q到抛物线C的准线的距离为．

    (Ⅰ)求抛物线C的方程；

    (Ⅱ)是否存在点M，使得直线MQ与抛物线C相切于点M？若存在，求出点M的坐标；若不存在，说明理由；

    (Ⅲ)若点M的横坐标为，直线l：y＝kx＋与抛物线C有两个不同的交点A，B，l与圆Q有两个不同的交点D，E，求当≤k≤2时，|AB|2＋|DE|2的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本小题16分）已知点A(-1, 0)、B(1, 0),△ABC的周长为2＋2.记动点C的轨迹

    为曲线W.

    (1)直接写出W的方程（不写过程）；

    (2)经过点（0, ）且斜率为k的直线l与曲线W 有两个不同的交点P和Q，是否存在常数k，使得向量与向量共线？如果存在，求出k的值；如果不存在，请说明理由.

    （3）设W的左右焦点分别为F1、 F2，点R在直线l：x－y＋8＝0上．当∠F1RF2取最大值时，求的值.

    查看答案和解析>>

    同步练习册答案