
 现有四分之一圆形的纸板(如图),∠AOB=90°,圆半径为1,要裁剪成四边形OAPB,且满足AP∥OB,,∠POA=θ,记此四边形的面积为f(θ),求f(θ)的最大值.
现有四分之一圆形的纸板(如图),∠AOB=90°,圆半径为1,要裁剪成四边形OAPB,且满足AP∥OB,,∠POA=θ,记此四边形的面积为f(θ),求f(θ)的最大值. 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
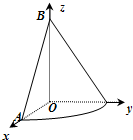 如图,直角三角形OAB的直角顶点O是空间坐标系O-xyz的原点,点A在Ox轴正半轴上,|OA|=1;点B在Oz轴正半轴上,|OB|=2.我们称△OAB绕Oz轴逆时针旋转
如图,直角三角形OAB的直角顶点O是空间坐标系O-xyz的原点,点A在Ox轴正半轴上,|OA|=1;点B在Oz轴正半轴上,|OB|=2.我们称△OAB绕Oz轴逆时针旋转| π |
| 2 |
| A、该四分之一圆锥体主视图和左视图的图形是全等的直角三角形 | ||
B、该四分之一圆锥体俯视图的图形是一个圆心角为
| ||
| C、该四分之一圆锥体主视图、左视图和俯视图的图形都是扇形 | ||
| D、该四分之一圆锥体主视图的图形面积大于俯视图的图形面积 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 现有四分之一圆形的纸板(如图),∠AOB=90°,圆半径为1,要裁剪成四边形OAPB,且满足AP∥OB,,∠POA=θ,记此四边形的面积为f(θ),求f(θ)的最大值.
现有四分之一圆形的纸板(如图),∠AOB=90°,圆半径为1,要裁剪成四边形OAPB,且满足AP∥OB,,∠POA=θ,记此四边形的面积为f(θ),求f(θ)的最大值.查看答案和解析>>
科目:高中数学 来源:2014届辽宁省五校协作体高一下期中考试数学试卷(解析版) 题型:解答题
(本小题满分12分)
现有四分之一圆形的纸板(如图), ,圆半径为
,圆半径为 ,要裁剪成四边形
,要裁剪成四边形 ,且满足
,且满足 ,
,
 ,
, ,记此四边形的面积为
,记此四边形的面积为 ,求
,求 的最大值.
的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com