
思路分析:要证直线MN∥平面PBC,只需证明MN∥平面PBC内的一条直线或MN所在的某个平面∥平面PBC.
证法一:过N作NR∥DC交PC于点R,连结RB,依题意得 ![]() =
=![]() =
=![]() =
=![]() =
=![]()
![]() NR=MB.
NR=MB.
∵NR∥DC∥AB,
∴四边形MNRB是平行四边形.
∴MN∥RB.
又∵RB![]() 平面PBC,
平面PBC,
∴直线MN∥平面PBC.
证法二:过N作NQ∥AD交PA于点Q,连结QM,
∵![]() =
=![]() =
=![]() ,
,
∴QM∥PB.
又NQ∥AD∥BC,
∴平面MQN∥平面PBC.
∴直线MN∥平面PBC.
证法三:过N作NR∥DC交PC于点R,连结RB,依题意有![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,![]() =
=![]() +
+![]() +
+![]() =
=![]() .
.
∴MN∥RB.
又∵RB![]() 平面PBC,∴直线MN∥平面PBC.
平面PBC,∴直线MN∥平面PBC.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2012-2013学年广东省湛江市高三8月第一次月考理科数学试卷(解析版) 题型:解答题
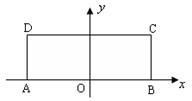
(本小题满分14分)已知长方形 ,
,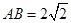 ,
,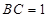 ,以
,以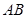 的中点
的中点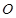 为
为
原点建立如图所示的平面直角坐标系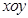 .
.
(1)求以A、B为焦点,且过C、D两点的椭圆的标准方程;
(2)设椭圆上任意一点为P,在x轴上有一个动点Q(t,0),其中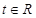 ,探究
,探究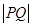 的最
的最
小值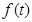 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com