练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设P是椭圆=1在第一象限部分的弧AB上的一点，求使四边形OAPB的面积最大的点P的坐标.

    思路分析：由于P是椭圆=1在第一象限部分的弧AB上的一动点，因此四边形OAPB的形状不定，则不能用特殊四边形的面积公式来求其最值，只能考虑把四边形分解为几个三角形，利用三角形的知识来求其面积的最大值.

    解：∵点P是椭圆=1在第一象限部分的弧AB上的一点,

    ∴设P(6cosθ,2sinθ),θ∈(0,)(图略).

    法一:直线AB方程为=1,即x+3y-6=0.欲使SOAPB最大,只需P到AB的距离最大.

    ∵dP-AB=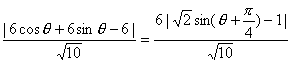θ∈(0,),

    ∴sin(θ+)＞0.∴当θ=时,dmax=.

    ∴(S△APB)max==6(-1).

    ∴(SOAPB)max=·6·2+6(-1)=.

    法二:SOAPB=S△POA+S△POB=·2·6cosθ+·6·2sinθ

    =6(sinθ+cosθ)=sin(θ+),θ∈(0,),

    ∴当θ=时,(SOAPB)max=,此时点P的坐标为(,2).

        拓展延伸 分析本题所求的最值可以有几个转化方向，即转化为求S△POA+S△POB，SOAPB的最大值或者求点P到AB的最大距离，或者求SOAPB的最大值.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知中心在原点、焦点在x轴上的椭圆的离心率是
    		3
    2
    ，椭圆上任意一点到两个焦点距离之和为4．
    （1）求椭圆标准方程；
    （2）设椭圆长轴的左端点为A，P是椭圆上且位于第一象限的任意一点，AB∥OP，点B在椭圆上，R为直线AB与y轴的交点，证明：
    AB
    •
    AR
    =2
    OP
    2    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

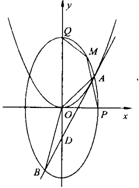    精英家教网已知点D（0，-2），过点D作抛线C1：x2=2py（p＞0）的切线l，切点A在第一象限，如图．
    （1）求切点A的纵坐标；
    （2）若离心率为
    		3
    2
    的椭圆C：
    y2
    a 2
    +
    x2
    b2
    =1（a＞b＞0）恰好经过切点A，设切线l交椭圆的另一点为B，记切线l，OA，OB的斜率分别为k，k2，k3，若2k1+k2=3k，求抛物线C1和椭圆C2的方程．
    （3）设P、Q分别是（2）中的椭圆C2的右顶点和上顶点，M是椭圆C2在第一象限的任意一点，求四边形OPMQ面积的最大值以及此时M点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在平面直角坐标系xOy中，抛物线C：y2=8x的焦点为F．椭圆Σ的中心在坐标原点，离心率e=
    1
    2
    ，并以F为一个焦点．
    （1）求椭圆Σ的标准方程；
    （2）设A1A2是椭圆Σ的长轴（A1在A2的左侧），P是抛物线C在第一象限的一点，过P作抛物线C的切线，若切线经过A1，求证：tan∠A1PA2=
    		2
    ．

    查看答案和解析>>

    科目：高中数学 来源：山东省实验中学2011届高三5月针对性练习数学理综试题 题型：044

    已知点D(0，－2)，过点D作抛线C1：x2＝2py(p＞0)的切线l，切点A在第一象限，如图．

    (1)求切点A的纵坐标；

    (2)若离心率为的椭圆恰好经过切点A，设切线l交椭圆的另一点为B，记切线l，OA，OB的斜率分别为k，k1，k2，若2k1＋k2＝3k，求抛物线C1和椭圆C2的方程．

    (3)设P、Q分别是(2)中的椭圆C2的右顶点和上顶点，M是椭圆C2在第一象限的任意一点，求四边形OPMQ面积的最大值以及此时M点的坐标．

    查看答案和解析>>

    同步练习册答案