
如图5,正方体![]() 的棱长为a,
的棱长为a,
E为DD1的中点.
(1)求证:BD1//平面EAC;
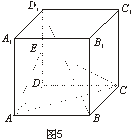 (2)求点D1到平面EAC的距离.
(2)求点D1到平面EAC的距离.
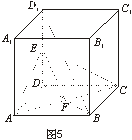 (1)证明:如图5,连接BD交AC于F,连EF. (1分)
(1)证明:如图5,连接BD交AC于F,连EF. (1分)
因为F为正方形ABCD对角线的交点,
所长F为AC、BD的中点. (3分)
在DDD1B中,E、F分别为DD1、DB的中点,
所以EF//D1B. (5分)
又EFÌ平面EAC,所以BD1//平面EAC. (7分)
(2)解1:设D1到平面EAC的距离为d.
在DEAC中,EF^AC,且![]() ,
,![]() ,
,
所以![]() ,
,
于是![]() . (9分)
. (9分)
因为![]() , (11分)
, (11分)
又![]() ,即
,即![]() , (13分)
, (13分)
解得![]() ,故D1到平面EAC的距离为
,故D1到平面EAC的距离为![]() . (14分)
. (14分)
解2:因为![]() ,
,![]() ,所以
,所以![]() 平面
平面![]()
又![]() 平面ACE,故平面
平面ACE,故平面![]() 平面ACE
平面ACE
过D作DM![]() ,交EF和
,交EF和![]() 于M和G,所以MG
于M和G,所以MG![]() 平面ACE(9分)
平面ACE(9分)
由(1)可知![]() ,所以GM是
,所以GM是![]() 到平面ACE的距离,也就是
到平面ACE的距离,也就是![]() 到平面ACE的距离(10分)
到平面ACE的距离(10分)
在![]() 中,因为
中,因为![]() ,即
,即![]()
所以,![]() ,(13分)
,(13分)
故![]() ,即D1到平面EAC的距离为
,即D1到平面EAC的距离为![]() . (14分)
. (14分)
解3:因为![]() ,F为AC这中点,所以
,F为AC这中点,所以![]() 且
且![]()
设![]() 到平面ACE的距离为d,
到平面ACE的距离为d,
因为![]() ,即
,即![]()
也就是![]() ,所以
,所以![]()
因为![]() 到平面ACE的距离与
到平面ACE的距离与![]() 到平面ACE的距离相等,
到平面ACE的距离相等,
所以,D1到平面EAC的距离为![]() . (10分)
. (10分)


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:高中数学 来源: 题型:
A.4 B
查看答案和解析>>
科目:高中数学 来源: 题型:
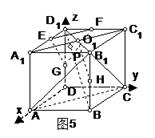
如图5:正方体ABCD-A1B1C1D1,过线段BD1上一点P(P![]() 平面ACB1)作垂直于D1B的平面分别交过D1的三条棱于E、F、G.
平面ACB1)作垂直于D1B的平面分别交过D1的三条棱于E、F、G.
(1)求证:平面EFG∥平面A CB1,并判断三角形类型;
(2)若正方体棱长为a,求△EFG的最大面积,并求此时EF与B1C的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点。已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是 ( )
 A 4;
A 4;
B 5;
C 6;
D 7;
查看答案和解析>>
科目:高中数学 来源:2010-2011年安徽省高一第二学期期中考试数学试卷 题型:选择题
有一塔形几何体由若干个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点。已知最底层正方体的棱长为2,且该塔形的表面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是

A. 4 B .5 C .6 D .7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com