
| A. | (0,$\frac{1}{e}$) | B. | (0,$\frac{1}{2e}$) | C. | (-∞,$\frac{1}{2e}$) | D. | ($\frac{1}{2e}$,$\frac{1}{e}$) |
分析 函数f(x)=$\left\{\begin{array}{l}{\frac{1}{x},x<0}\\{\frac{lnx}{x},x>0}\end{array}\right.$,若函数F(x)=f(x)-kx在R上有3个零点,当x>0时,令f(x)=0,有两个实数解.可得k=$\frac{lnx}{{x}^{2}}$即直线y=k和g(x)=$\frac{lnx}{{x}^{2}}$有两个交点.x<0时有一个交点,求出g(x)的导数和单调区间,可得最值和端点处的函数值,即可得到所求k的范围.
解答 解:函数f(x)=$\left\{\begin{array}{l}{\frac{1}{x},x<0}\\{\frac{lnx}{x},x>0}\end{array}\right.$,若函数F(x)=f(x)-kx在R上有3个零点,当x>0时,令f(x)=0,有两个实数解.可得k=$\frac{lnx}{{x}^{2}}$即直线y=k和g(x)=$\frac{lnx}{{x}^{2}}$有两个交点.
由g′(x)=$\frac{1-2lnx}{{x}^{3}}$,令1-2lnx=0,可得x=$\sqrt{e}$,可得g(x)在(0,$\sqrt{e}$),函数是增函数,
在($\sqrt{e}$,+∞)递减,
即有g(x)在x=$\sqrt{e}$取得最大值$\frac{1}{2e}$;
直线y=k和函数g(x)的图象有两个交点.k∈(0,$\frac{1}{2e}$),
函数F(x)=f(x)-kx在R上有3个零点,x<0时y=k和g(x)=$\frac{1}{x}$有一个交点,k∈(0,$\frac{1}{2e}$),
显然成立.
实数k的取值范围为(0,$\frac{1}{2e}$).
故选:B.
点评 本题考查函数的零点问题的解法,注意运用转化思想,构造函数法和导数求得单调区间、最值,考查运算能力,属于中档题.


科目:高中数学 来源:2017届山东潍坊临朐县高三10月月考数学(理)试卷(解析版) 题型:解答题
某企业共有20条生产线,由于受生产能力和技术水平等因素的影响,会产生一定量的次品.根据经验知道,每台机器产生的次品数 万件与每台机器的日产量
万件与每台机器的日产量 万件
万件 之间满足关系:
之间满足关系: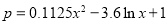 .已知每生产1万件合格的产品可以以盈利3万元,但每生产1万件次品将亏损1万元.
.已知每生产1万件合格的产品可以以盈利3万元,但每生产1万件次品将亏损1万元.
(Ⅰ)试将该企业每天生产这种产品所获得的利润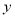 表示为
表示为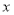 的函数;
的函数;
(Ⅱ)当每台机器的日产量为多少时,该企业的利润最大,最大为多少?
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(文)试卷(解析版) 题型:解答题
已知曲线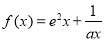 (
(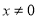 ,
, )在
)在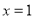 处的切线与直线
处的切线与直线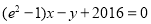 平行.
平行.
(1)讨论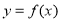 的单调性;
的单调性;
(2)若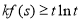 在
在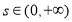 ,
,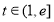 上恒成立,求实数
上恒成立,求实数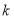 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2017届湖南长沙长郡中学高三上周测十二数学(文)试卷(解析版) 题型:选择题
一个空间几何体的三视图如图所示,其中正视图为等腰直角三角形,侧视图与俯视图为正方形,则该几何体的体积为( )
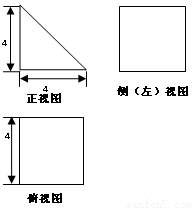
A.64 B.32
C.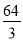 D.
D.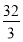
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1] | B. | (-∞,1) | C. | [1,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com