

(1) ![]() 与
与![]() 所成的角;
所成的角;
(2)P点到平面EFB的距离;
(3)异面直线PM与FQ的距离.
解:建立空间直角坐标系,使得D(0,0,0)、A(a,0,0)、B(a,a,0)、C(0,a,0)、M(0,0,a)、E(a,0,a)、F(0,a,a),则由中点坐标公式得P(![]() ,0,
,0,![]() )、Q(
)、Q(![]() ,
,![]() ,0).
,0).
(1)∴![]() =(-
=(-![]() ,0,
,0,![]() ),
), ![]() =(
=(![]() ,-
,-![]() ,-a),
,-a), ![]() ·
·![]() =(-
=(-![]() )×
)×![]() +0+
+0+![]() ×(-a)=
×(-a)=![]() a2,
a2,
且|![]() |=
|=![]() a,|
a,| ![]() |=
|=![]() a.
a.
∴cos〈![]() ,
,![]() 〉=
〉= =
= =-
=-![]() .
.
故得两向量所成的角为150°.
(2)设n=(x,y,z)是平面EFB的单位法向量,即|n|=1,n⊥平面EFB,
∴n⊥![]() ,n⊥
,n⊥![]() .又
.又![]() =(-a,a,0),EB=(0,a,-a),即有
=(-a,a,0),EB=(0,a,-a),即有 得其中的一组解
得其中的一组解
∴n=(![]() ,
,![]() ,
,![]() ),
),![]() =(
=(![]() ,0,
,0,![]() ).
).
设所求距离为d,则d=|![]() ·n|=
·n|=![]() a.
a.
(3)设e=(x1,y1,z1)是两异面直线的公垂线上的单位方向向量,则由![]() =(-
=(-![]() ,0,
,0,![]() ),
), ![]() =(
=(![]() ,-
,-![]() ,-a),得
,-a),得
 求得其中的一个e=(
求得其中的一个e=(![]() ,-
,-![]() ,
,![]() ),而
),而![]() =(0,a,0).
=(0,a,0).
设所求距离为m,则m=|![]() ·e|=|-
·e|=|-![]() a|=
a|=![]() a.
a.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:黄冈中学 高一数学(下册)、第五章 平面向量单元(5.1~5.5)测试卷 题型:044
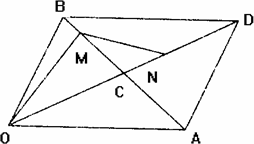
如图所示,已知四边形OADB是以向量![]() ,
,![]() 为边的平行四边形,其中
为边的平行四边形,其中![]() ,
,![]() .试以向量a,b为一组基底,表示出向量
.试以向量a,b为一组基底,表示出向量![]() 、
、![]() 、
、![]() .
.
查看答案和解析>>
科目:高中数学 来源:数学教研室 题型:044
(1)异面直线PM与FQ所成的角;
(2)四面体P-EFB的体积;
(3)异面直线PM与FQ的距离.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西赣州四所重点中学高三上学期期末联考文数学试卷(解析版) 题型:解答题
如图所示,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点。

(Ⅰ)求证:平面FGH⊥平面AEB;
(Ⅱ)在线段PC上是否存在一点M,使PB⊥平面EFM?若存在,求出线段PM的长;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com