
在正方体ABCD-A1B1C1D1中,M是棱AB的中点.

(1)求证:BC∥平面A1MD1;
(2)求二面角A1-D1M-C的大小.
|
解法1:(1)∵BC∥B1C1,B1C1∥A1D1,∴BC∥A1D1. 又A1D1 ∴BC∥平面A1MD1; 5分 (2)设平面A1MD1与棱DC相交于点N, 连结D1N,则点N是DC的中点. ∴A1D1⊥平面D1DCC1,A1D1 ∴平面A1MND1⊥平面D1DCC1, 且D1N是交线. 过点C作CH⊥D1N于H点, 则CH⊥平面A1MND1, 再过H作HO⊥D1M于O点, 连结CO,根据三垂线定理得CO⊥D1M, 从而∠COH是二面角C-D1M-N, 也就是所求二面角A1-D1M-C的补二面角的平面角 8分 设正方体的棱长为2,则在 所以有 在 又由于可求得 所以在 进而有 根据三角形面积公式得 从而在 因此所求的二面角
解法2:分别以直线DA、DC、DD1为x、y、z轴建立空间直角坐标系D-xyz,并设 正方体的棱长为2,则相关点的坐标分别为 A1(2,0,2),D1(0,0,2),C(0,2,0),M(2,1,0) 6分 再设 令 设 即 |


科目:高中数学 来源: 题型:
(本小题满分12分)
在正方体ABCD-A′B′C′D′中,点M是棱AA′的中点,点O是对角线BD′的中点.

 (Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅱ)求二面角M-BC′-B′的大小;
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
在正方体ABCD-A′B′C′D′中,点M是棱AA′的中点,点O是对角线BD′的中点.
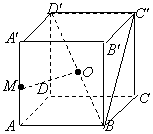
 (Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅱ)求二面角M-BC′-B′的大小;
查看答案和解析>>
科目:高中数学 来源:2010年高考试题(四川卷)解析版(文) 题型:解答题
在正方体ABCD-A′B′C′D′中,点M是棱AA′的中点,点O是对角线BD′的中点.

 (Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅱ)求二面角M-BC′-B′的大小;
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com