
解析:小河看成一条直线l,A、B两村在小河同侧,且|AO|=300 m,|BB′|=700 m,|AB|=500 m.根据题意,应在l上选一点P,使|PA|+|PB|最小,根据平面几何知识,在A、B的另一岸取点A的对称点A′,连结A′B,则A′B与小河交点P即为所求(通过两边之和大于第三边可证).因此,问题转化为,在已知条件下计算|PA|+|PB|的最小值问题.以小河l所在直线为x轴,y轴通过A点,建立直角坐标系,如下图所示作A关于x轴的对称点A′,连结A′B,A′B与x轴交于P点,则P点即为所求,即|PA|+|PB|为最小(若在l上任取一点P′PA,则|P′B|+|A′B|.
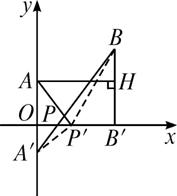
∵|A′P|=|AP|,∴|P′A|+|P′B|>|AP|+|PB|.
∴根据已知条件,A(0,300),A′(0,-300).
过B作BB′⊥x轴于点B′,
过A作AH⊥BB′于H.
∵|AO|=300,|BB′|=700,∴|BH|=400.
又|AB|=500,
∴|AH|=300求得B点坐标B(300,700),
∴直线A′B的方程为![]() ,即y=
,即y=![]() x-300.
x-300.
∴P点坐标即为直线A′B与x轴交点的坐标(90,0).即|OP|=90 m.
即水电站应建立在河边距A到小河最近点的90 m处用料最省.
物指数般的繁殖和生长.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com