
在△ABC中,角A、B、C的对边分别为a、b、c,若
(Ⅰ)求证:A=B;
(Ⅱ)求边长c的值;
(Ⅲ)若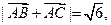 求△ABC的面积.
求△ABC的面积.
解:(Ⅰ)∵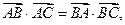 ∴bccosA=accosB,即bcosA=acosB.
∴bccosA=accosB,即bcosA=acosB.
由正弦定理得 sinBcosA=sinAcosB, ∴sin(A-B)=0. ∵-π<A-B<π, ∴A-B=0,∴A=B. --------------------(4分)
∵-π<A-B<π, ∴A-B=0,∴A=B. --------------------(4分)
(Ⅱ)∵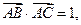 ∴bccosA=1. 由余弦定理得
∴bccosA=1. 由余弦定理得 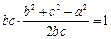 ,即b2+c2-a2=2.
,即b2+c2-a2=2.
∵由(Ⅰ)得a=b,∴c2=2,∴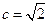 . --------------------(8分)
. --------------------(8分)
(Ⅲ)∵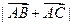 =,∴
=,∴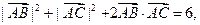 即c2+b2+2=6,
即c2+b2+2=6,
∴c2+b2=4. ∵c2=2, ∴ b2=2,即b=
b2=2,即b= . ∴△ABC为正三角形.
. ∴△ABC为正三角形.
∴ 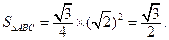 ----------------------(12分)
----------------------(12分)
解析


科目:高中数学 来源: 题型:
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 11 | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| b |
| a |
| sinB |
| cosA |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com