练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    将等差数列3，8，13，18，…按顺序抄在练习本上，已知每行抄13个数，每页抄21行．求数33 333所在的页和行．

    答案：略
    解析：

    解：每页共13×21＝273个数字，33333＝3＋(n－1)×5，则n＝6667，即33333为第6667个数，由整除概念可知33333在第25页第9行．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    将n2个正整数1，2，3，…，n2填入n×n方格中，使其每行、每列、每条对角线上的数的和都相等，这个正方形叫做n阶幻方．记f（n）为n阶幻方对角线上数的和，如右图就是一个3阶幻方，可知f（3）=15．已知将等差数列：3，4，5，…前16项填入4×4方格中，可得到一个4阶幻方，则其对角线上数的和f（4）等于（　　）
    8 3 4
    1 5 9
    6 7 2
    A、36B、42C、34D、44

    查看答案和解析>>

    科目：高中数学 来源： 题型：

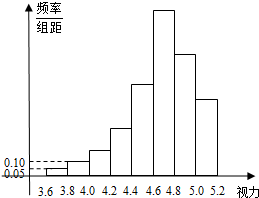    为了解某校高三学生的视力情况，随机地抽查了该校100名高三学生的视力，按视力情况分成8组，得到如图所示的频率分布直方图，但不慎将部分数据丢失，只知道前6组的频数从左到右依次是等比数列{an}的前六项，后3组的频数从左到右依次是等差数列{bn}的前三项．
    （1）求数列{an}和{bn}的通项公式；
    （2）设数列{cn}满足cn=
    35-bn3an
    ，求数列{cn}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    第一行是等差数列0，1，2，3，…，2008，将其相邻两项的和依次写下作为第二行，第二行相邻两项的和依次写下作为第三行，依此类推，共写出2008行．
    0，1，2，3，…，2005，2006，2007，2008
    1，3，5，…，4011，4013，4015
    4，8，…，8024，8028
    …
    （1）由等差数列性质知，以上数表的每一行都是等差数列．记各行的公差组成数列{di}（i=1，2，3…，2008）．求通项公式di；
    （2）各行的第一个数组成数列{bi}（1，2，3，…，2008），求数列{bi}所有各项的和．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    将n2个正整数1，2，3，…，n2填入n×n方格中，使其每行、每列、每条对角线上的数的和都相等，这个正方形叫做n阶幻方．记f（n）为n阶幻方对角线上数的和，如右图就是一个3阶幻方，可知f（3）=15．已知将等差数列：3，4，5，…前16项填入4×4方格中，可得到一个4阶幻方，则其对角线上数的和f（4）等于（　　）
    8 3 4
    1 5 9
    6 7 2
    A．36B．42C．34D．44

    查看答案和解析>>

    科目：高中数学 来源：浙江省学军中学2010届高三上学期第四次月考（理） 题型：选择题

     将连续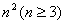个正整数填入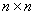的方格中，使其每行、每列、每条对角线上的各数

    8

    3

    4

    1

    5

    9

    6

    7

    2

    之和都相等，这个正方形叫做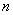阶幻方数阵，记为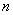阶幻方数阵对角线上

    各数之和，如图就是一个3阶幻方数阵，可知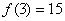。若将等差数列3，4，5，6，的前16 项填入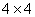方格中，可得到一个4阶幻方数阵，则  （     ）

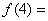     A．44         B．42          C．40        D．36

     

    查看答案和解析>>

    同步练习册答案