
如果函数y=f(x)满足f(a+x)=f(a-x),则f(x)的图象关于直线x=a对称.
|
解:设P(x0,y0)是函数y=f(x)的图象上的任意一点,则有y0=f(x0),易知点P(x0,y0)关于x=a的对称点为 f(2a-x0)=f[a+(a-x0)]=f[a-(a-x0)]=f(x0)=y0. 故点 由点P的任意性可知,y=f(x)的图象是关于直线x=a对称的. |
|
分析:对于曲线关于直线的对称问题,通常转化为点关于直线的对称问题去解决,本题只需在y=f(x)上任取一点P(x0,y0),若P关于x=a的对称点 解题心得:1.点关于直线对称的点,两点连线的斜率与对称轴垂直且中点在对称轴上. 2.曲线关于直线的对称问题都可转化为点关于直线的对称问题,这实际上是化难为易原则的运用. |


科目:高中数学 来源:2006-2007年上学期许昌市高三数学四校联考(附答案) 题型:013
已知命题P:函数y=loga(ax+2a)(a>0且a≠1)的图像必过定点(-1,1);命题q:如果函数y=f(x-3)的图像关于原点对称,那么函数y=f(x)的图像关于(3,0)点对称,则
A.“P且q”为真
B.“P或q”为假
C.P真q假
D.P假q真
查看答案和解析>>
科目:高中数学 来源:江西新余市第一中学2012届高三第一次模拟考试数学理科试题 题型:013
函数y=![]() (x)是函数y=f(x)的导函数,且函数y=f(x)在点P(x0,f(x0))处的切线为l:y=g(x)=
(x)是函数y=f(x)的导函数,且函数y=f(x)在点P(x0,f(x0))处的切线为l:y=g(x)=![]() (x0)(x-x0)+f(x0),F(x)=f(x)-g(x),如果函数y=f(x)在区间[a,b]上的图象如图所示,且a<x0<b,那么正确的是
(x0)(x-x0)+f(x0),F(x)=f(x)-g(x),如果函数y=f(x)在区间[a,b]上的图象如图所示,且a<x0<b,那么正确的是

![]() (x0)=0,x=x0是F(x)的极大值点
(x0)=0,x=x0是F(x)的极大值点
![]() (x0)=0,x=x0是F(x)的极小值点
(x0)=0,x=x0是F(x)的极小值点
![]() (x0)≠0,x=x0不是F(x)极值点
(x0)≠0,x=x0不是F(x)极值点
![]() (x0)≠0,x=x0是F(x)极值点
(x0)≠0,x=x0是F(x)极值点
查看答案和解析>>
科目:高中数学 来源:湖北省武汉市武昌区2012届高三5月调研考试数学文科试题 题型:013
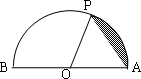
已知点P在半径为1的半圆周上沿着A→P→B路径运动,设弧![]() 的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论:
的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论:
①函数y=f(x)的定义域和值域都是[0,π];
②如果函数y=f(x)的定义域R,则函数y=f(x)是周期函数;
③如果函数y=f(x)的定义域R,则函数y=f(x)是奇函数;
④函数y=f(x)在区间[0,π]上是单调递增函数.
以上结论的正确个数是
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省高三上学期期中考试理科数学 题型:解答题
(13分)下图为三角函数 (A>0,ω>0,
(A>0,ω>0, )图象的一段.
)图象的一段.
(1)求函数的解析式及 的值;
的值;
(2)如果函数y=f (x)-m在( ,
,
 )内有且仅有一个零点,求实数m的取值范围.
)内有且仅有一个零点,求实数m的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com