
分析 ①通过x=y=1,即可求解f(1)的值,通过令x=y=-1,即可求解f(-1)的值.
②令x=-1,用-x换y,化简方程,即可证明函数是偶函数.
解答 解:①函数y=f(x)对任意实数x、y∈R满足:f(x•y)=f(x)+f(y)+1,
令x=y=1,可得:f(1)=f(1)+f(1)+1,可得f(1)=-1,
令x=y=-1可得:f(1)=f(-1)+f(-1)+1,
解得f(-1)=-1.
②证明:令x=-1,-x换y,可得f(x)=f(-1)+f(-x)+1=f(-x),
即f(-x)=f(x).
函数y=f(x)在R上是偶函数.
点评 本题考查抽象函数的应用,赋值法的应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{3π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
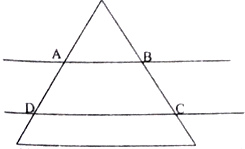 将边长为4正三角形薄片,用平行于底边的两条直线剪成三块(如图所示),这两条平行线间的距离为$\sqrt{3}$,其中间一块是梯形记为ABCD,记$S=\frac{{{{({梯形ABCD的周长})}^2}}}{梯形ABCD的面积}$,则S的最小值为$\frac{32\sqrt{3}}{3}$.
将边长为4正三角形薄片,用平行于底边的两条直线剪成三块(如图所示),这两条平行线间的距离为$\sqrt{3}$,其中间一块是梯形记为ABCD,记$S=\frac{{{{({梯形ABCD的周长})}^2}}}{梯形ABCD的面积}$,则S的最小值为$\frac{32\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知实数x,y的取值如表所示.
已知实数x,y的取值如表所示.| x | 0 | 1 | 2 | 3 | 4 |
| y | 1 | 2 | 4 | 6 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com