Question

10．命题p：关于x的方程x|x|-2x+m=0（m∈R）有三个实数根；命题q：0≤m＜1；则命题p成立是命题q成立的（　　）

• A． 充分而不必要的条件
• B． 必要而不充分的条件
• C． 充要条件
• D． 既不充分又不必要的条件

Answer 1

分析 根据充分条件和必要条件的定义结合函数和方程之间的关系进行判断即可．

解答 解：由方程 $x|x|-2x+m=0⇒m=x（2-|x|）=\left\{\begin{array}{l}x（2-x），x≥0\\ x（2+x），x＜0\end{array}\right.$，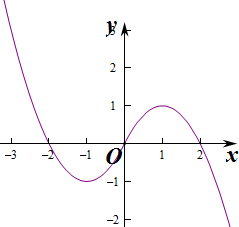
易知函数f（x）是R上的奇函数，由f（x）的图象可知，函数f（x）在[0，+∞）上的最大值是1，
根据图象的对称性知函数f（x）在（-∞，0）上的最小值为-1，
又函数f（x）的图象与x轴有3个交点，
那么原方程有3个实数根的充要条件是（-1，1），而[0，1）?（-1，1），
故选：B

点评 本题主要考查充分条件和必要条件的判断，以及函数与方程之间的关系，利用数形结合是解决本题的关键．