练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB=2，AF=1，M是线段EF的中点.?

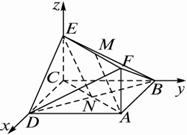
    求证：(1)AM∥平面BDE；

    (2)AM⊥平面BDF.

     

    证明：(1)建立如图所示的空间直角坐标系，

    设AC∩BD=N，连结NE.?

    则点N、E的坐标分别为(,,0)、(0,0,1).?

    ∴=(-,-,1).?

    又点A、M的坐标分别是(2,2,0)、(,,1),∴=(-,-,1).?

    ∴=且NE与AM不共线.?

    ∴NE∥AM.?

    又∵NE平面BDE，AM 平面BDE,

    ∴AM∥平面BDE.

    (2)同(1)，AM=(-,-,1),

    ∵D(2,0,0),F(2,2,1),?

    ∴=(0,2,1).∴·=0.?

    ∴⊥.?

    同理, ⊥.?

    又DF∩BF=F，∴AM⊥平面BDF.?

    温馨提示：用向量知识证立体几何问题仍需判定(或性质)定理.欲证线面平行只需证线线平行；欲证线面垂直需证线线垂直.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

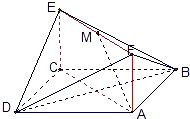    精英家教网如图，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB=
    		2
    ，AF=1，M是线段EF的中点．
    （Ⅰ）求证AM∥平面BDE；
    （Ⅱ）求二面角A-DF-B的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，已知正方形ABCD的边长为1，过正方形中心O的直线MN分别交正方形的边AB，CD于M，N，则当
    MN
    BN
    最小时，CN=
    		5
    -1
    2
    		5
    -1
    2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，已知正方形ABCD和梯形ACEF所在平面互相垂直，AB=2，AF=
    		2
    ，CE=2
    		2
    ，CE∥AF，AC⊥CE，
    ME
    =2
    FM

    （I）求证：CM∥平面BDF；
    （II）求异面直线CM与FD所成角的余弦值的大小；
    （III）求二面角A-DF-B的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，已知正方形ABCD和矩形ACEF所在的平面互相垂直，AB=
    		2
    ，AF=1    ．
    （1）求二面角A-DF-B的大小；
    （2）在线段AC上找一点P，使PF与AD所成的角为60°，试确定点P的位置．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•深圳二模）如图，已知正方形ABCD在水平面上的正投影（投影线垂直于投影面）是四边形A′B′C′D′，其中A与A'重合，且BB′＜DD′＜CC′．
    （1）证明AD′∥平面BB′C′C，并指出四边形AB′C′D′的形状；
    （2）如果四边形中AB′C′D′中，AD′=
    		2
    ，AB′=
    		5
    ，正方形的边长为
    		6
    ，求平面ABCD与平面AB′C′D′所成的锐二面角θ的余弦值．

    查看答案和解析>>

    同步练习册答案