Question

设定点M(-3,4),动点N在圆x²+y²=4上运动,以OM、ON为两边作平行四边形MONP,求点P的轨迹.

Answer 1

思路分析:本题关键是找出点P与定点M及已知动点N之间的联系,用平行四边形对角线互相平分这一定理即可.

解:如图4-1-3所示,设P(x,y),N(x₀,y₀),线段OP的中点坐标为(),线段MN的中点坐标为().

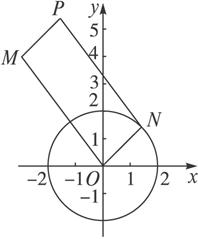
图4-1-3

因为平行四边形对角线互相平分,

故,

从而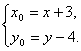.N(x+3,y-4)在圆上,

故(x+3)²+(y-4)²=4.因此所求轨迹为圆:(x+3)²+(y-4)²=4,

但应除去两点()和().

  绿色通道:如果动点P(x,y)的轨迹依赖于另一动点(a,b)的轨迹,而Q(a,b)又在已知曲线上,则可先列出关于x,y,a,b的方程组,利用x,y表示出a,b,把a,b代入已知曲线方程便可得动点P的轨迹方程,此法称为相关点法(亦称代入法或转移法).