Question

（）（本小题满分12分）

数列{a_n}的前N项和为S_n,a₁=1,a_n+1=2S_n (n∈N*).

(I)求数列{a_n}的通项a_n;

(II)求数列｛na_n｝的前n项和T.

An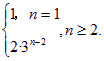swer 1

a_n=, T_n=+(n-)3^n-1(n∈N*)

解析:

解：（I）∵a_n+1=2S_n,,

∴S_n+1-S_n=2S_n,

∴=3.

又∵S₁＝a₁=1,

∴数列｛S_n｝是首项为1、公比为3的等比数列，S_n=3^n-1(n∈N*).

∴当n2时，a_n-2S_n-1=2·3^n-2(n2),

∴a_n=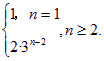

(II)T_n=a₁+2a₂+3a₃+…+na_n.

当n=1时，T1=1;

当n2时，Tn=1+4·3⁰+6·3¹+2n·3 ^n-2,…………①

3T_n=3+4·3¹+6·3²+…+2n·3^n-1,…………②

①-②得：-2T_n=-2+4+2(3¹+3²+…+3^n-2)-2n·3 ^n-1

                                          =2+2·

                     =-1+(1-2n)·3^n-1

∴T_n=+(n-)3^n-1   (n2).

又∵T_n=a1=1也满足上式，

∴T_n=+(n-)3^n-1(n∈N*)