练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．函数f（x）=x3+ax-2在区间[1，+∞）内是增函数，则实数a的取值范围是[-3，+∞）．

    分析 求函数的导数，根据函数的单调性和导数之间的关系即可得到结论．

    解答 解：∵函数f（x）=x3+ax-2在区间[1，+∞）上单调递增，
    ∴f′（x）=3x2+a≥0，在区间[1，+∞）恒成立，
    即a≥-3x2，
    ∵-3x2≤-3，
    ∴a≥-3，
    故实数a的取值范围是[-3，+∞）．
    故答案为：[-3，+∞）

    点评 本题主要考查函数单调性和单调区间的应用，求函数的导数利用导数研究单调性是解决本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    8．某商场举行抽奖促销活动，在该商场消费的顾客按如下规则参加抽奖活动：
    消费金额X（元）[500，1000）[1000，1500）[1500，+∞）
    抽奖次数124
    抽奖中有9个大小形状完全相同的小球，其中4个红球、3个白球、2个黑球（每次只能抽取一个，且不放回抽取），若抽得红球，获奖金10元；若抽得白球，获奖金20元；若抽得黑球，获奖金40元，
    （1）若某顾客在该商场当日消费金额为2000元，求该顾客获得奖金70元的概率；
    （2）若某顾客在该商场当日消费金额为1200元，获奖金ξ元．求ξ的分布列和E（ξ）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知z∈C，且|z+3-4i|=1，则|z|的最大值为6，最小值为4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．在△ABC中，角A，B，C所对的边分别为a，b，c，已知a=1，且（1-b）（sinA+sinB）=（c-b）sinC，则△ABC周长的最大值为3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知集合A={x|x2-16＜0}，B={x|x2-4x+3＞0}，求A∪B，A∩（∁RB）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知圆锥的底面半径为1，母线长与底面的直径相等，则该圆锥的体积为$\frac{{\sqrt{3}π}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

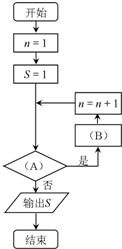    10．已知数列{an}，a1=1，an+1=an+n，计算数列{an}的第20项．现已给出该问题算法的程序框图（如图所示）．为使之能完成上述的算法功能，则在如图判断框中（A）处和（B）处依次应填上合适的语句是（　　）
    A．n≤20，S=S-nB．n≤20，S=S+nC．n≤19，S=S-nD．n≤19，S=S+n

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

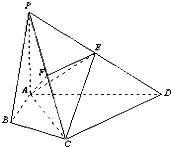    7．在四棱锥P-ABCD中，∠ABC=∠ACD=90°，∠BAC=∠CAD=60°，PA⊥平面ABCD，E为PD的中点，PA=2AB=2．
    （1）若F为PC的中点，求证：PC⊥平面AEF；
    （2）求点F到平面ACE的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知t为实数，函数f（x）=（x2-4）（x-t）且f′（-1）=0，则t等于（　　）
    A．0B．-1C．$\frac{1}{2}$D．2

    查看答案和解析>>

    同步练习册答案