
四棱锥
P-ABCD的底面是边长为a的正方形,PB垂直面ABCD,证明无论四棱锥的高怎样变化,面PAD与面PCD所成的二面角恒大于90°.|
解析:注意到题目中所给的二面角,面PAD与面PCD的棱为PD,围绕PD而考虑问题解决途径. 证法一:利用定义法 经 A在PDA平面内作AE⊥PD于E,连CE.
因底是正方形,故 CD=DA.△CED≌△AED,AE=EC,∠CED=∠AED=90°, 则CE⊥PD. 故∠CEA是面PAD与面PCD所成二面角的平面角. 设AC与BD交于O,连EO,则EO⊥AC. 因 cos∠AEC= 所以面PAD与面PCD所成的二面角恒大于90°. 证法二:运用三垂线法 ∵PB⊥面ABCD,则PB⊥AD,又AD⊥AB, ∴AD⊥面PAB,即面PAB⊥面PAD. 过B作BE⊥PA,则BE⊥面PAD. 在面PBC内作PG
经 C作CF⊥面PAD于F, 那么连结EF,有EF 经F作FH⊥PD于H,连CH, 则∠FHC是所求二面角平面角的补角. 因CF⊥FH,故∠FHC是锐角. 则面PAD与面PCD所成二面角大于90°. 此结论证明过程中与棱锥高无关. 证法三:利用垂面法找平面角. 在证法一所给图形中 连AC、BD,因AC⊥BD,PB⊥面ABCD, ∴AC⊥PD. 经A作AE⊥PD于E,那么有PD⊥面AEC,连CE, 即PD⊥CE. 故PD与平面AEC垂直后,面AEC与面ADC及面ADP的交线EA、EC构成角∠CEA就是二面角的平面角. 以下同证法一. |


科目:高中数学 来源: 题型:
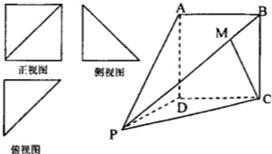 一个四棱锥P一ABCD的正视图是边长为2的正方形及其一条对角线,侧视图和俯视图全全等的等腰直角三角形,直角边长为2,直观图如图.
一个四棱锥P一ABCD的正视图是边长为2的正方形及其一条对角线,侧视图和俯视图全全等的等腰直角三角形,直角边长为2,直观图如图.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•湖北模拟)如图,已知四棱锥P一ABCD的底面为直角梯形,AB∥CD,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
(2012•湖北模拟)如图,已知四棱锥P一ABCD的底面为直角梯形,AB∥CD,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
[2012·永春一中二模] 四棱锥P-ABCD的顶点P在底面ABCD上的投影恰好是A,其正视图与侧视图都是腰长为a的等腰直角三角形.则在四棱锥P-ABCD的任意两个顶点的连线中,互相垂直的异面直线共有________对.
查看答案和解析>>
科目:高中数学 来源:2014届山西省高二第一次月考文科数学试卷(解析版) 题型:选择题
如右图所示,正四棱锥P-ABCD的底面积为3,体积为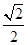 ,E为侧棱PC的中点,则PA与BE所成的角为( )
,E为侧棱PC的中点,则PA与BE所成的角为( )

A. 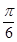 B.
B.
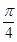 C.
C.
 D.
D.
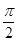
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省高三上学期第二次月考理科数学试卷 题型:解答题
如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2, 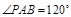 ,
, .
.
(1)求证:平面 平面
平面 ;
;
(2)求三棱锥D-PAC的体积;
(3)求直线PC与平面ABCD所成角的正弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com