练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，设三角形ABC的三个顶点在平面的同侧，A⊥于，B⊥于，C⊥于，G、分别是△ABC和△的重心，求证：G⊥

    证明见解析


    解析:

    连接AG并延长交BC于D，连并延长交于 ，连D、G，由于 A⊥，B⊥，C⊥，则A∥B∥C因为，所以G∥A，因此G⊥

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图，直角三角形ABC中，∠B=90°，AB=1，BC=
    		3
    ．点M，N分别在边AB和AC 上（M点和B点不重合），将△AMN沿MN翻折，△AMN变为△A′MN，使顶点A′落在边BC上（A′点和B点不重合）．设∠AMN=θ．
    （1）用θ表示∠BA′M和线段AM的长度，并写出θ的取值范围；
    （2）求线段AN长度的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

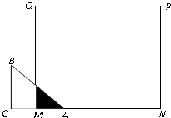    已知如图，等腰三角形ABC的直角边长为a，正方形MNPQ的边为b （a＜b），C、M、A、N在同一条直线上，开始时点A与点M重合，让△ABC向右移动，最后点C与点N重合．设三角形与正方形的重合面积为y，点A移动的距离为x，则y关于x的大致图象是（　　）

    查看答案和解析>>

    科目：高中数学 来源：2012年人教A版高中数学必修二2.3直线、平面垂直的判定及其性质练习卷（二） 题型：解答题

    如图，设三角形ABC的三个顶点在平面的同侧，A⊥于，B⊥于，C⊥于，G、分别是△ABC和△的重心，求证：G⊥

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，设三角形ABC的三个顶点在平面的同侧，A⊥于，B⊥于，C⊥于，G、分别是△ABC和△的重心，求证：G⊥

    查看答案和解析>>

    同步练习册答案