
(08年江西卷)如图,正三棱锥![]() 的三条侧棱
的三条侧棱![]() 、
、![]() 、
、![]() 两两垂直,且长度均为2.
两两垂直,且长度均为2.![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,![]() 是
是![]() 的中点,过
的中点,过![]() 的平面与侧棱
的平面与侧棱![]() 、
、![]() 、
、![]() 或其延长线分别相交于
或其延长线分别相交于![]() 、
、![]() 、
、![]() ,已知
,已知![]() .
.
(1)求证:![]() ⊥面
⊥面![]() ;
;
(2)求二面角![]() 的大小.
的大小.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
(08年江西卷理)如图1,一个正四棱柱形的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块,容器内盛有![]() 升水时,水面恰好经过正四棱锥的顶点P。如果将容器倒置,水面也恰好过点
升水时,水面恰好经过正四棱锥的顶点P。如果将容器倒置,水面也恰好过点![]() (图2)。有下列四个命题:
(图2)。有下列四个命题:
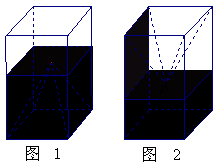
A.正四棱锥的高等于正四棱柱高的一半
B.将容器侧面水平放置时,水面也恰好过点![]()
C.任意摆放该容器,当水面静止时,水面都恰好经过点![]()
D.若往容器内再注入![]() 升水,则容器恰好能装满
升水,则容器恰好能装满
其中真命题的代号是: (写出所有真命题的代号).
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年江西卷)如图,正三棱锥![]() 的三条侧棱
的三条侧棱![]() 、
、![]() 、
、![]() 两两垂直,且长度均为2.
两两垂直,且长度均为2.![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,![]() 是
是![]() 的中点,过
的中点,过![]() 的平面与侧棱
的平面与侧棱![]() 、
、![]() 、
、![]() 或其延长线分别相交于
或其延长线分别相交于![]() 、
、![]() 、
、![]() ,已知
,已知![]() .
.
(1)求证:![]() ⊥面
⊥面![]() ;
;
(2)求二面角![]() 的大小.
的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com