已知函数f(x)对于一切x、y∈R,都有f(xy)=f(x+y)+f(x-y).
(Ⅰ)求证:f(x)在R上是偶函数;
(Ⅱ)若f(x)在区间(-∞,0)上是减函数,且有f(2a2+a+1)<f(-2a2+4a-3),求实数a的取值范围.
(Ⅰ)证明:函数f(x)对于一切x、y∈R,都有f(xy)=f(x+y)+f(x-y),
令x=0,得f(0)=f(y)+f(-y),…(1分)
再令y=x,得f(0)=f(x)+f(-x).…①…(2分)
令y=0,得f(0)=f(x)+f(x).…②…(3分)
①-②得f(-x)-f(x)=0,…(4分)
∴f(-x)=f(x).…(5分)
故f(x)在R上是偶函数.…(6分)
(Ⅱ)解:因为f(x)在R上是偶函数,
所以f(x)的图象关于y轴对称.…(7分)
又因为f(x)在区间(-∞,0)上是减函数,
所以f(x)在区间(0,+∞)上是增函数.…(8分)
∵
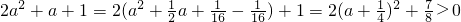
,
-2a
2+4a-3=-2(a
2-2a+1-1)-3=-2(a-1)
2-1<0,
∴2a
2-4a+3>0.…(9分)
∵f(-2a
2+4a-3)=f(2a
2-4a+3).
原不等式可化为f(2a
2+a+1)<f(2a
2-4a+3)…(10分)
∴2a
2+a+1<2a
2-4a+3.解之得a<

.…(11分)
故实数a的取值范围是
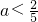
.…(12分)
分析:(Ⅰ)由题意利用赋值法:先令x=0,可得f(0)=f(y)+f(-y),然后再令y=x,得f(0)=f(x)+f(-x),利用赋值求出f(0)即可求证
(Ⅱ)由(I)知f(x)在R上是偶函数,及已知f(x)在区间(-∞,0)上是减函数,结合偶函数对称区间上的单调性相反可知f(x)在区间(0,+∞)上是增函数,从而可求不等式
点评:本题主要考查了抽象函数的函数值的求解,解题的关键是利用赋值法,偶函数的对称区间上的单调性的应用,及利用函数的单调性求解不等式,具有一定的综合性

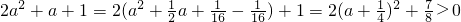 ,
, .…(11分)
.…(11分)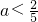 .…(12分)
.…(12分)
