已知:函数f(x)=x3+px2+9qx+p+q+3 (x∈R)的图象关于原点对称,其中p,q是实常数.
(1)求p,q的值;
(2)确定函数f(x)在区间[-3,3]上的单调性;
(3)若当-3≤x≤3时,不等式f(x)≥10sint-49恒成立,求实数t的取值范围.
解:(1)由f(-x)=-f(x),得2px
2+2(p+q+3)=0恒成立,∴p=0,q=-3.
(2)f(x)=x
3-27x,取-3≤x
1<x
2≤3,则x
12+x
1x
2+x
22<27.
∴f(x
1)-f(x
2)=(x
1-x
2)(x
12+x
1x
2+x
22-27)>0,f(x)在[-3,3]为减函数.
(3)由(2)知f(x)在区间[-3,3]上的最小值为f(3)=-54,
∴只需f(3)=-54≥10sint-49,
由
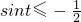
,得
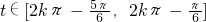
(k∈Z).
分析:(1)利用奇函数的性质,得2px
2+2(p+q+3)=0恒成立,求得p,q的值
(2)利用单调性的定义,可证明函数f(x)在区间[-3,3]上为减函数
(3)先求出函数f(x)在区间[-3,3]上的最小值,再令10sint-49比所求最小值不大,解不等式即可
点评:本题考查了函数的奇偶性、单调性和不等式恒成立问题,解题时要熟练掌握函数奇偶性、单调性定义,能准确利用函数单调性求函数值域

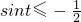 ,得
,得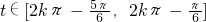 (k∈Z).
(k∈Z).

 阅读快车系列答案
阅读快车系列答案