
(1)作此函数在一个周期开区间上的简图;
(2)求出此函数的定义域、周期和单调区间;
(3)写出此函数图象的渐近线方程和所有对称中心的坐标.
思路分析:解决本题的关键是利用换元法(令![]() -
-![]() =z)将问题转化到正切函数y=tanZ的图象和性质上处理,在这里体现出了化归这一重要的数学思想方法.
=z)将问题转化到正切函数y=tanZ的图象和性质上处理,在这里体现出了化归这一重要的数学思想方法.
解:(1)列表:
x | - | … | - |
|
| … |
|
| - | … |
| 0 |
| … |
|
tan( | -∞ | … | -1 | 0 | 1 | … | +∞ |
描点作线画图:
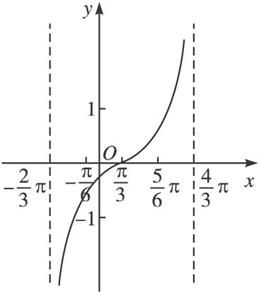
(2)∵![]() -
-![]() ≠
≠![]() +kπ,k∈Z.
+kπ,k∈Z.
∴x≠![]() +2kπ,从而函数的定义域是{x∈R|x≠
+2kπ,从而函数的定义域是{x∈R|x≠![]() π+2kπ,k∈Z}.
π+2kπ,k∈Z}.
函数的周期是T=![]() =2π.
=2π.
又∵-![]() +kπ<
+kπ<![]() -
-![]() <
<![]() +kπ,k∈Z,
+kπ,k∈Z,
∴-![]() +2kπ<x<
+2kπ<x<![]() π+2kπ.
π+2kπ.
故函数的单调增区间是
(-![]() +2kπ,
+2kπ,![]() π+2kπ),k∈Z;无减区间.
π+2kπ),k∈Z;无减区间.
(3)由![]() -
-![]() =
=![]() +kπ,k∈Z得
+kπ,k∈Z得
x=![]() ,
,
故函数图象的渐近线为
x=![]() π+2kπ,k∈Z;
π+2kπ,k∈Z;
再由![]() -
-![]() =
=![]() ,k∈Z,
,k∈Z,
得x=![]() +kπ,
+kπ,
故函数图象的对称中心为(![]() +kπ,0),k∈Z.
+kπ,0),k∈Z.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com