
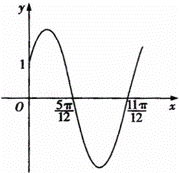
已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<![]() )的部分图象如图所示.
)的部分图象如图所示.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)求函数g(x)=f(x﹣![]() )﹣f(x+
)﹣f(x+![]() )的单调递增区间.
)的单调递增区间.
考点:
由y=Asin(ωx+φ)的部分图象确定其解析式;三角函数中的恒等变换应用;复合三角函数的单调性.
专题:
计算题.
分析:
(I)先利用函数图象求此函数的周期,从而计算得ω的值,再将点(![]() ,0)和(0,1)代入解析式,分别解得φ和A的值,最后写出函数解析式即可;
,0)和(0,1)代入解析式,分别解得φ和A的值,最后写出函数解析式即可;
(II)先利用三角变换公式将函数g(x)的解析式化为y=Asin(ωx+φ)型函数,再将内层函数看做整体,置于外层函数即正弦函数的单调增区间上,即可解得函数g(x)的单调增区间
解答:
解:(I)由图象可知,周期T=2(![]() ﹣
﹣![]() )=π,∴ω=
)=π,∴ω=![]() =2
=2
∵点(![]() ,0)在函数图象上,∴Asin(2×
,0)在函数图象上,∴Asin(2×![]() +φ)=0
+φ)=0
∴sin(![]() +φ)=0,∴
+φ)=0,∴![]() +φ=π+2kπ,即φ=2kπ+
+φ=π+2kπ,即φ=2kπ+![]() ,k∈z
,k∈z
∵0<φ<![]()
∴φ=![]()
∵点(0,1)在函数图象上,∴Asin![]() =1,A=2
=1,A=2
∴函数f(x)的解析式为f(x)=2sin(2x+![]() )
)
(II)g(x)=2sin[2(x﹣![]() )+
)+![]() ]﹣2sin[2(x+
]﹣2sin[2(x+![]() )+
)+![]() ]=2sin2x﹣2sin(2x+
]=2sin2x﹣2sin(2x+![]() )
)
=2sin2x﹣2(![]() sin2x+
sin2x+![]() cos2x)=sin2x﹣
cos2x)=sin2x﹣![]() cos2x
cos2x
=2sin(2x﹣![]() )
)
由﹣![]() +2kπ≤2x﹣
+2kπ≤2x﹣![]() ≤
≤![]() +2kπ,k∈z
+2kπ,k∈z
得kπ﹣![]() ≤x≤kπ+
≤x≤kπ+![]()
∴函数g(x)=f(x﹣![]() )﹣f(x+
)﹣f(x+![]() )的单调递增区间为[kπ﹣
)的单调递增区间为[kπ﹣![]() ,kπ+
,kπ+![]() ]k∈z
]k∈z
点评:
本题主要考查了y=Asin(ωx+φ)型函数的图象和性质,根据图象求函数的解析式,利用函数解析式求复合三角函数单调区间的方法,属基础题


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| a-x2 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com