
已知双曲线的焦点在x轴上,离心率为2,F1、F2为左、右焦点.P为双曲线上一点,且∠F1PF2=60°,S△PF1F2=12![]() ,求双曲线的标准方程.
,求双曲线的标准方程.
|
解:如图,设双曲线方程为
因为e= 由双曲线的定义||PF1|-|PF2||=2a=c, 在△PF1F2中,由余弦定理,得 |F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|cos60° =(|PF1|-|PF2|)2+2|PF1||PF2|(1-cos60°), 即4c2=c2+|PF1||PF2|.① 又 所以 即|PF1||PF2|=48.② 由①②,得c2=16,c=4,则a=2,b2=c2-a2=12. 所以所求的双曲线方程为 解析:要求双曲线的标准方程,可设出方程 |
|
遇到过椭圆、双曲线的两焦点与曲线上任一点组成的三角形时,常用定义与解三角形知识解决相关问题.本题要注意整体代换的运算技巧. |


科目:高中数学 来源: 题型:
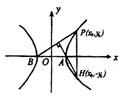 已知双曲线的焦点在x轴上,且过点A(1,0)和B(-1,0),P是双曲线上异于A、B的任一点,如果△APB的垂心H总在双曲线上,求双曲线的标准方程.
已知双曲线的焦点在x轴上,且过点A(1,0)和B(-1,0),P是双曲线上异于A、B的任一点,如果△APB的垂心H总在双曲线上,求双曲线的标准方程.查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 4 |
| y2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省宜春市上高二中高二(下)第五次月考数学试卷(理科)(解析版) 题型:选择题
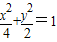 的右焦点作x轴的垂线交椭圆于A、B两点,已知双曲线的焦点在x轴上,对称中心在坐标原点且两条渐近线分别过A、B两点,则双曲线的离心率是( )
的右焦点作x轴的垂线交椭圆于A、B两点,已知双曲线的焦点在x轴上,对称中心在坐标原点且两条渐近线分别过A、B两点,则双曲线的离心率是( )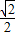
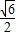

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com