
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=![]() a,点E在PD上,且PE∶ED=2∶1.
a,点E在PD上,且PE∶ED=2∶1.

(1)证明PA⊥平面ABCD.
(2)在棱PC上是否存在一点F,使BF∥平面AEC?
|
证明:(1)∵ABCD是菱形,∠ABC=60°, ∴AB=AD=AC=a. 在△PAB中,由PA2+AB2=2a2=PB2, ∴PA⊥AB.同理,PA⊥AD. ∴PA⊥平面ABCD. (2)如图,以A为坐标原点,直线AD、AP分别为y轴、z轴,过A点垂直平面PAD的直线为x轴,建立空间直角坐标系,则由已知得
A(0,0,0),B( ∴ 设点F是棱PC上的点, 令 即λ= 方法二:设平面AEC的法向量为n=(x,y,z), 则 令y=1,则z=-2,x= 即n=( 由BF∥平面AEC,得n⊥ ∴ 解得λ= 即当F是棱PC的中点时,BF∥平面AEC. |
|
判定线面垂直,可以用判定定理.第(2)问为开放型问题,解决此类问题通常是先假设符合条件的点存在,然后利用已知条件推理求解.从而得出结论. |


 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案科目:高中数学 来源: 题型:
 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在底面是菱形的四棱锥S-ABCD中,∠ABC=60°,SA=AB=a,SB=SD=
如图,在底面是菱形的四棱锥S-ABCD中,∠ABC=60°,SA=AB=a,SB=SD=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2.
如图,在底面是菱形的四棱锥 P-ABCD中,∠ABC=60°,PA⊥平面ABCD,点E、F、G分别为CD、PD、PB的中点.PA=AD=2.查看答案和解析>>
科目:高中数学 来源: 题型:
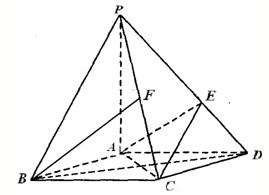 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=2,PB=PD=2
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=2,PB=PD=2| 2 |
| PE |
| PD |
| π |
| 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com