
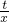 有如下性质:如果常数t>0,那么该函数(0,
有如下性质:如果常数t>0,那么该函数(0, ]上是减函数,在[
]上是减函数,在[ ,+∞)上是增函数.
,+∞)上是增函数. ,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域.
,x∈[0,1],利用上述性质,求函数f(x)的单调区间和值域. =2x+1+
=2x+1+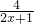 -8,
-8,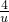 -8,u∈[1,3],由已知性质得,
-8,u∈[1,3],由已知性质得, 时,f(x)单调递减,所以递减区间为[0,
时,f(x)单调递减,所以递减区间为[0, ]
] ≤x≤1时,f(x)单调递增,所以递增区间为[
≤x≤1时,f(x)单调递增,所以递增区间为[ ,1]
,1] )=-4,f(1)=-
)=-4,f(1)=- ,得f(x)的值域为[-4,-3]
,得f(x)的值域为[-4,-3]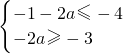 所以 a=
所以 a=


科目:高中数学 来源: 题型:
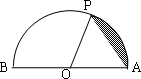
 (2012•武昌区模拟)已知点P在半径为1的半圆周上沿着A→P→B路径运动,设弧 的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论:
(2012•武昌区模拟)已知点P在半径为1的半圆周上沿着A→P→B路径运动,设弧 的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论:查看答案和解析>>
科目:高中数学 来源:湖北省武汉市武昌区2012届高三5月调研考试数学文科试题 题型:013
已知点P在半径为1的半圆周上沿着A→P→B路径运动,设弧![]() 的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论:
的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论:
①函数y=f(x)的定义域和值域都是[0,π];
②如果函数y=f(x)的定义域R,则函数y=f(x)是周期函数;
③如果函数y=f(x)的定义域R,则函数y=f(x)是奇函数;
④函数y=f(x)在区间[0,π]上是单调递增函数.
以上结论的正确个数是
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 已知点P在半径为1的半圆周上沿着A→P→B路径运动,设弧 的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论:
已知点P在半径为1的半圆周上沿着A→P→B路径运动,设弧 的长度为x,弓形面积为f(x)(如图所示的阴影部分),则关于函数y=f(x)的有如下结论:查看答案和解析>>
科目:高中数学 来源:2012年湖北省武汉市武昌区高三五月调考数学试卷(文科)(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com