
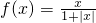


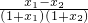


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2010年上海市徐汇区高考数学二模试卷(理科)(解析版) 题型:解答题
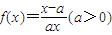
查看答案和解析>>
科目:高中数学 来源:2010年上海市徐汇区、金山区高考数学二模试卷(理科)(解析版) 题型:解答题
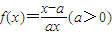
查看答案和解析>>
科目:高中数学 来源:2013届江苏省高二下学期期中考试文科数学试卷(解析版) 题型:解答题
(16分)已知函数 .
.
(1)判断并证明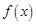 的奇偶性;
的奇偶性;
(2)求证: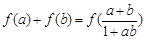 ;
;
(3)已知a,b∈(-1,1),且 ,
, ,求
,求 ,
, 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2010年上海市徐汇区高三第二次模拟考试数学卷(理) 题型:解答题
(满分16分;第(1)小题5分,第(2)小题5分,第三小题6分)
已知函数 
(1)判断并证明 在
在 上的单调性;
上的单调性;
(2)若存在 ,使
,使 ,则称
,则称 为函数
为函数 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值,并求出不动点
的值,并求出不动点 ;
;
(3)若 在
在 上恒成立 , 求
上恒成立 , 求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com