练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    抛物线的焦点为椭圆
    x2
    9
    +
    y2
    4
    =1的左焦点，顶点在椭圆中心，则抛物线方程为______．
    因为椭圆
    x2
    9
    +
    y2
    4
    =1的左焦点为（-
    		5
    .0），所以
    p
    2
    =
    		5
    ，2p=4
    		5
    且抛物线开口向左．
    所以抛物线方程为y2=-4
    		5
    x．
    故答案为：y2=-4
    		5
    x．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2009-2010学年广州市七区联考高二数学（文）下学期期末监测 题型：解答题

    （本大题满分14分)

    如图，已知直线L：过椭圆C：的右焦点F，

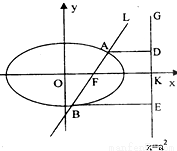
    且交椭圆C于A、B两点，点A、B在直线上的射影依次为点D、E.

    （Ⅰ）若抛物线的焦点为椭圆C的上顶点，求椭圆C的方程；

    （Ⅱ）若为x轴上一点；

    求证: A、N、E三点共线.

     

     

     

     

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

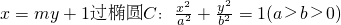    如图，已知直线L：数学公式的右焦点F，且交椭圆C于A、B两点，点A、B在直线G：x=a2上的射影依次为点D、E．
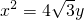    （1）若抛物线数学公式的焦点为椭圆C 的上顶点，求椭圆C的方程；（2）（理科生做）连接AE、BD，试探索当m变化时，直线AE、BD是否相交于一定点N？若交于定点N，请求出N点的坐标，并给予证明；
    否则说明理由．
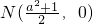    （文科生做）若数学公式为x轴上一点，求证：数学公式．

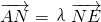    查看答案和解析>>

    科目：高中数学 来源：四川省月考题 题型：解答题

    如图，已知直线L：x=my+1过椭圆C：的右焦点F，且交椭圆C于A，B两点，点A，F，B在直线G：x=a2上的射影依次为点D，K，E，
    （1）已知抛物线的焦点为椭圆C的上顶点．
    ①求椭圆C的方程；
    ②若直线L交y轴于点M，且，当m变化时，求λ1+λ2的值；
    （2）连接AE，BD，试探索当m变化时，直线AE、BD是否相交于一定点N？若交于定点N，请求出N点的坐标并给予证明；否则说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2010年安徽省安庆市潜山中学高考数学模拟试卷（解析版） 题型：解答题

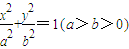    如图，已知直线L：x=my+1过椭圆C：的右焦点F，且交椭圆C于A，B两点，点A，F，B在直线G：x=a2上的射影依次为点D，K，E，
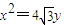    （1）已知抛物线的焦点为椭圆C的上顶点．
    ①求椭圆C的方程；
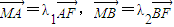    ②若直线L交y轴于点M，且，当m变化时，求λ1+λ2的值；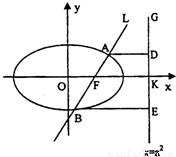
    （2）连接AE，BD，试探索当m变化时，直线AE、BD是否相交于一定点N？若交于定点N，请求出N点的坐标并给予证明；否则说明理由．

    查看答案和解析>>

    科目：高中数学 来源：2011年辽宁省沈阳市东北育才学校高考数学模拟试卷（文科）（解析版） 题型：解答题

    如图，已知直线L：的右焦点F，且交椭圆C于A、B两点，点A、B在直线G：x=a2上的射影依次为点D、E．
    （1）若抛物线的焦点为椭圆C的上顶点，求椭圆C的方程；
    （2）若为x轴上一点，求证：．

    查看答案和解析>>

    同步练习册答案