
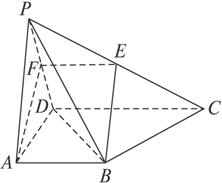
图2-3-27
(1)证明:BE∥平面PAD;
(2)平面EBD能垂直于平面ABCD吗,为什么?
思路分析:证线面平行,只要证出线平行于面内的一条直线即可.由E为PC的中点,所以取PD的中点F.
(1)证明:如图2-3-28,取PD的中点F,连结EF、AF,则EF∥CD,且CD=2EF.

图2-3-28
又∵AB∥CD,CD=2AB,∴EF∥AB且EF=AB.
∴四边形ABEF是平行四边形.
∴AF∥BE.而AF![]() 平面PAD.∴BE∥平面PAD.
平面PAD.∴BE∥平面PAD.
(2)解:如图2-3-29假设平面EBD能垂直于底面ABCD,过点E作EO⊥BD于点O,连结AO、CO.

图2-3-29
∵面BDE∩面ABCD=BD,且EO![]() 面BDE,∴EO⊥面ABCD.
面BDE,∴EO⊥面ABCD.
又∵PA⊥面ABCD,直线AC是PC在面ABCD上的射影,
∴平面ABCD的一条斜线PC上点E在面ABCD内的射影O在直线AC上.
同时,EO∥PA.又E为PC的中点,
∴O为AC的中点.由AB∥CD可知△ABO∽△CDO,且相似比为![]() =
=![]() .
.
∴AB=CD.这与已知条件四边形ABCD为梯形,且CD=2AB矛盾.
∴假设“平面BDE⊥平面ABCD”是不成立的.
因此,平面BDE不能垂直于平面ABCD.
绿色通道:解答探索性问题时,可从假设命题成立入手,若导出矛盾,说明假设不成立;若导不出矛盾,说明假设成立.


科目:高中数学 来源: 题型:
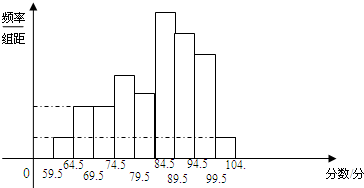 为了了解某校毕业班数学考试情况,抽取了若干名学生的数学成绩,将所得的数据经过整理后,画出频率分布直方图(如图所示).已知从左到右第一组的频率是0.03,第二组的频率是0.06,第四组的频率是0.12,第五组的频率是0.10,第六组的频率是0.27,且第四组的频数是12,则
为了了解某校毕业班数学考试情况,抽取了若干名学生的数学成绩,将所得的数据经过整理后,画出频率分布直方图(如图所示).已知从左到右第一组的频率是0.03,第二组的频率是0.06,第四组的频率是0.12,第五组的频率是0.10,第六组的频率是0.27,且第四组的频数是12,则查看答案和解析>>
科目:高中数学 来源: 题型:
 11、某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.
11、某校为了了解学生的身体素质情况,对初三(2)班的50名学生进行了立定跳远、铅球、100米三个项目的测试,每个项目满分为10分.如图,是将该学生所得的三项成绩(成绩均为整数)之和进行整理后,分成5组画出的频率分布直方图,已知从左至右前4个小组的频率分别为0.02,0.1,0.12,0.46.查看答案和解析>>
科目:高中数学 来源: 题型:
为了了解某校毕业班数学考试情况,抽取了若干名学生的数学成绩,将所得的数据经过整理后,画出频率分布直方图(如图所示)。已知从左到右第一组的频率是0.03,第二组的频率是0.06,第四组的频率是0.12,第五组的频率是0.10,第六组的频率是0.27,且第四组的频数是12,则
(1)所抽取的学生人数是多少?
(2)那些组出现的学生人数一样多?出现人数最多的组有多少人?
(3)若分数在85分以上(含85分)的为优秀,试估计数学成绩的优秀率是多少?

查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省株洲二中高三(下)第十次月考数学试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com