练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    将1，2，3……，20这二十个数分成甲，乙两组，使甲组各数的平均数比乙组各数的平均数大1，且甲，乙两组的平均数均为正整数，则甲组有    ▲    个数．

         10  

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （09 年聊城一模理）（12分）

    某校有一贫困学生因病需手术治疗，但现在还差手术费万元，团委计划在全校开展爱心募捐活动，为了增加活动的趣味性吸引更多学生参与，特举办“摇奖100%中奖”活动.凡捐款10元者，享受一次摇奖机会，如图是摇奖机的结构示意图，摇奖机的旋转盘是均匀的，扇形区域所对应的圆心角的比值分别为1：2：3：4：5.相应区域分别设立一、二、三、四、五等奖，奖品分别为价值分别为5元、4元、3元、2元、1元的学习用品.摇奖时，转动圆盘片刻，待停止后，固定指针指向哪个区域（边线忽略不计）即可获得相应价值的学习用品（如图指针指向区域，可获得价值3元的学习用品）.

    （Ⅰ）预计全校捐款10元者将会达到1500人次，那么除去

    购买学习用品的款项后，剩余款项是否能帮助该生完成手术治疗？

    （II）如果学生甲捐款20元，获得了两次摇奖机会，求他获得价

    值6元的学习用品的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数F(n)=n，n=1，2，3，4，5，6，试用计算机语言将F(3)，F(4)，F(5)向后移一个位置，使F(3)空出来且F(3)＝0从而形成新的对应关系，使用语言正确的是　　（　　）

        A．F(6)=F(5)，F(5)=F(4)，F(4)=F(3)，F(3)=0

        B．F(3)=F(4)，F(4)=F(5)，F(5)=F(6)，F(3)=0

        C．F(3)=0，F(6)=F(5)，F(5)=F(4)，F(4)=F(3)

        D．F(3)=0，F(4)=F(5)，F(5)=F(6)，F(4)=F(3)

       

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某校有一贫困学生因病需手术治疗，但现在还差手术费万元，团委计划在全校开展爱心募捐活动，为了增加活动的趣味性吸引更多学生参与，特举办“摇奖100%中奖”活动.凡捐款10元者，享受一次摇奖机会，如图是摇奖机的结构示意图，摇奖机的旋转盘是均匀的，扇形区域所对应的圆心角的比值分别为1：2：3：4：5.相应区域分别设立一、二、三、四、五等奖，奖品分别为价值分别为5元、4元、3元、2元、1元的学习用品.摇奖时，转动圆盘片刻，待停止后，固定指针指向哪个区域（边线忽略不计）即可获得相应价值的学习用品（如图指针指向区域，可获得价值3元的学习用品）.

    （Ⅰ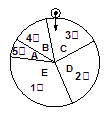）预计全校捐款10元者将会达到1500人次，那么除去

    购买学习用品的款项后，剩余款项是否能帮助该生完成手术治疗？

    （II）如果学生甲捐款20元，获得了两次摇奖机会，求他获得价

    值6元的学习用品的概率.

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年陕西省高三第十一次大练习理科数学（解析版） 题型：解答题

    某校有一贫困学生因病需手术治疗，但现在还差手术费万元，团委计划在全校开展爱心募捐活动，为了增加活动的趣味性吸引更多学生参与，特举办“摇奖100%中奖”活动.凡捐款10元者，享受一次摇奖机会，如图是摇奖机的结构示意图，摇奖机的旋转盘是均匀的，扇形区域所对应的圆心角的比值分别为1：2：3：4：5.相应区域分别设立一、二、三、四、五等奖，奖品分别为价值分别为5元、4元、3元、2元、1元的学习用品.摇奖时，转动圆盘片刻，待停止后，固定指针指向哪个区域（边线忽略不计）即可获得相应价值的学习用品（如图指针指向区域，可获得价值3元的学习用品）.

    （Ⅰ）预计全校捐款10元者将会达到1500人次，那么除去购买学习用品的款项后，剩余款项是否能帮助该生完成手术治疗？

    （II）如果学生甲捐款20元，获得了两次摇奖机会，求他获得价值6元的学习用品的概率.

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年山东省高考模拟预测数学文试卷（解析版） 题型：解答题

    一个袋中装有四个形状大小完全相同的球，球的编号分别为1，2，3，4．

    （I）从袋中随机抽取一个球，将其编号记为，然后从袋中余下的三个球中再随机抽取一个球，将其编号记为．求关于的一元二次方程有实根的概率；

    （II）先从袋中随机取一个球，该球的编号为m，将球放回袋中，然后再从袋中随机取一个球，该球的编号为n．若以 作为点P的坐标，求点P落在区域内的概率．

    【解析】第一问利用古典概型概率求解所有的基本事件数共12种，然后利用方程有实根，则满足△=4a2-4b2≥0，即a2≥b2。，这样求得事件发生的基本事件数为6种，从而得到概率。第二问中，利用所有的基本事件数为16种。即基本事件（m，n）有：（1，1）  （1,2）   （1,3）  （1,4）   （2,1）  （2，2）  （2,3）   （2,4）   （3,1）   （3,2）  （3，3）    （3,4）   （4,1）   （4,2）   （4,3）  （4，4）共16种。在求解满足的基本事件数为（1，1） （2,1）  （2，2） （3,1） 共4种，结合古典概型求解得到概率。

    （1）基本事件（a，b）有：（1,2）   （1,3）  （1,4）   （2,1）   （2,3）   （2,4）   （3,1）   （3,2）  （3,4）   （4,1）   （4,2）   （4,3）共12种。

    ∵有实根， ∴△=4a2-4b2≥0，即a2≥b2。

    记“有实根”为事件A，则A包含的事件有：（2,1）   （3,1）   （3,2）  （4,1）   （4,2）   （4,3） 共6种。

    ∴PA.= 。   …………………6分

    （2）基本事件（m，n）有：（1，1）  （1,2）   （1,3）  （1,4）   （2,1）  （2，2）  （2,3）   （2,4）   （3,1）   （3,2）  （3，3）    （3,4）   （4,1）   （4,2）   （4,3）  （4，4）共16种。

    记“点P落在区域内”为事件B，则B包含的事件有：

    （1，1） （2,1）  （2，2） （3,1） 共4种。∴PB.=

     

    查看答案和解析>>

    同步练习册答案