解法一:(Ⅰ)因为f(x)=x
2+alnx,所以

,
函数f(x)的图象在点P(1,f(1))处的切线斜率k=f'(1)=2+a.
由2+a=10得:a=8. …(4分)
(Ⅱ)由(Ⅰ)知,f(x)=x
2+8lnx,令F(x)=f(x)-2x=x
2-2x+8lnx.
因为F(1)=-1<0,F(2)=8ln2>0,所以F(x)=0在(0,+∞)至少有一个根.
又因为
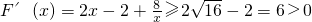
,所以F(x)在(0,+∞)上递增,
所以函数F(x)在(0,+∞)上有且只有一个零点,即方程f(x)=2x有且只有一
个实根. …(7分)
(Ⅲ)证明如下:
由f(x)=x
2+8lnx,

,可求得曲线y=f(x)在点A处的切
线方程为

,
即

(x>0). …(8分)
记h(x)=x
2+8lnx-

=x
2+8lnx-

(x>0),
则

. …(11分)
(1)当

,即t=2时,

对一切x∈(0.+∞)成立,
所以h(x)在(0,+∞)上递增.
又h(t)=0,所以当x∈(0,2)时h(x)<0,当x∈(2,+∞)时h(x)>0,
即存在点A(2,4+8ln2),使得曲线在点A附近的左、右两部分分别位于曲线
在该点处切线的两侧. …(12分)
(2)当

,即t>2时,

时,h'(x)>0;

时,h'(x)<0;x∈(t,+∞)时,h'(x)>0.
故h(x)在

上单调递减,在(t,+∞)上单调递增.
又h(t)=0,所以当

时,h(x)>0;当x∈(t,+∞)时,h(x)>0,
即曲线在点A(t,f(t))附近的左、右两部分都位于曲线在该点处切线的
同侧. …(13分)
(3)当

,即0<t<2时,x∈(0,t)时,h'(x)>0;

时,h'(x)<0;

时,h'(x)>0.
故h(x)在(0,t)上单调递增,在

上单调递减.
又h(t)=0,所以当x∈(0,t)时,h(x)<0;当

时,h(x)<0,
即曲线在点A(t,f(t))附近的左、右两部分都位于曲线在该点处切线的同侧.
综上,存在唯一点A(2,4+8ln2)使得曲线在点A附近的左、右两部分分别
位于曲线在该点处切线的两侧. …(14分)
解法二:(Ⅰ)(Ⅱ)同解法一;
(Ⅲ)证明如下:
由f(x)=x
2+8lnx,

,可求得曲线y=f(x)在点A处的切
线方程为

,
即

(x>0). …(8分)
记h(x)=x
2+8lnx-

=x
2+8lnx-

(x>0),
则

. …(11分)
若存在这样的点A(t,f(t)),使得曲线y=f(x)在该点附近的左、右两部分都
位于曲线在该点处切线的两侧,则问题等价于t不是极值点,
由二次函数的性质知,当且仅当

,即t=2时,t不是极值点,即h'(x)≥0.
所以h(x)在(0,+∞)上递增.
又h(t)=0,所以当x∈(0,2)时,h(x)<0;当x∈(2,+∞)时,h(x)>0,
即存在唯一点A(2,4+8ln2),使得曲线在点A附近的左、右两部分分别
位于曲线在该点处切线的两侧. …(14分)
分析:解法一:(Ⅰ)对函数f(x)求导,根据导数的几何意义可求f(x)的图象在点P(1,f(1))处的切线斜率k,结合已知可求a
(Ⅱ)令F(x)=f(x)-2x=x
2-2x+8lnx,利用函数的导数,判断函数F(x)在(0,+∞)上的单调性,结合F(1)=-1<0,F(2)=8ln2>0,可证
(Ⅲ)由导数的几何意义可求曲线y=f(x)在点A处的切线方程

(x>0),构造函数h(x)=x
2+8lnx-

=x
2+8lnx-

(x>0),对h(x)求导,通过讨论t的取值范围来判断h′(x)的符号,进而可判断h(x)在(0,+∞)上的单调性,即可判断
解法二:(Ⅰ)(Ⅱ)同解法一;
(Ⅲ)由导数的几何意义可求曲线y=f(x)在点A处的切线方程

(x>0),构造函数h(x)=x
2+8lnx-

=x
2+8lnx-

(x>0),对h(x)求导,若存在这样的点A(t,f(t)),使得曲线y=f(x)在该点附近的左、右两部分都位于曲线在该点处切线的两侧,则问题等价于t不是极值点,二次函数的性质可求
点评:本题主要考查函数、导数等基础知识,考查推理论证能力、运算求解能力,函数与方程思想、数形结合思想、考查化归与转化思想.

 ,
,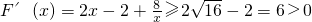 ,所以F(x)在(0,+∞)上递增,
,所以F(x)在(0,+∞)上递增, ,可求得曲线y=f(x)在点A处的切
,可求得曲线y=f(x)在点A处的切 ,
, (x>0). …(8分)
(x>0). …(8分) =x2+8lnx-
=x2+8lnx- (x>0),
(x>0), . …(11分)
. …(11分) ,即t=2时,
,即t=2时, 对一切x∈(0.+∞)成立,
对一切x∈(0.+∞)成立, ,即t>2时,
,即t>2时, 时,h'(x)>0;
时,h'(x)>0; 时,h'(x)<0;x∈(t,+∞)时,h'(x)>0.
时,h'(x)<0;x∈(t,+∞)时,h'(x)>0. 上单调递减,在(t,+∞)上单调递增.
上单调递减,在(t,+∞)上单调递增. 时,h(x)>0;当x∈(t,+∞)时,h(x)>0,
时,h(x)>0;当x∈(t,+∞)时,h(x)>0, ,即0<t<2时,x∈(0,t)时,h'(x)>0;
,即0<t<2时,x∈(0,t)时,h'(x)>0; 时,h'(x)<0;
时,h'(x)<0; 时,h'(x)>0.
时,h'(x)>0. 上单调递减.
上单调递减. 时,h(x)<0,
时,h(x)<0, ,可求得曲线y=f(x)在点A处的切
,可求得曲线y=f(x)在点A处的切 ,
, (x>0). …(8分)
(x>0). …(8分) =x2+8lnx-
=x2+8lnx- (x>0),
(x>0), . …(11分)
. …(11分) ,即t=2时,t不是极值点,即h'(x)≥0.
,即t=2时,t不是极值点,即h'(x)≥0. (x>0),构造函数h(x)=x2+8lnx-
(x>0),构造函数h(x)=x2+8lnx- =x2+8lnx-
=x2+8lnx- (x>0),对h(x)求导,通过讨论t的取值范围来判断h′(x)的符号,进而可判断h(x)在(0,+∞)上的单调性,即可判断
(x>0),对h(x)求导,通过讨论t的取值范围来判断h′(x)的符号,进而可判断h(x)在(0,+∞)上的单调性,即可判断 (x>0),构造函数h(x)=x2+8lnx-
(x>0),构造函数h(x)=x2+8lnx- =x2+8lnx-
=x2+8lnx- (x>0),对h(x)求导,若存在这样的点A(t,f(t)),使得曲线y=f(x)在该点附近的左、右两部分都位于曲线在该点处切线的两侧,则问题等价于t不是极值点,二次函数的性质可求
(x>0),对h(x)求导,若存在这样的点A(t,f(t)),使得曲线y=f(x)在该点附近的左、右两部分都位于曲线在该点处切线的两侧,则问题等价于t不是极值点,二次函数的性质可求

 阅读快车系列答案
阅读快车系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<