尖子生新课堂课时作业系列答案科目：高中数学 来源：2010-2011学年北京市西城区高三二模考试理科数学 题型：解答题
（（本小题满分13分）
若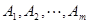
为集合
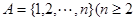且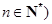
的子集，且满足两个条件：
①
；
②对任意的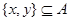
，至少存在一个
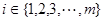，使
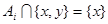或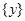
.
则称集合组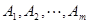具有性质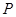
.
如图，作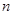
行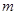
列数表，定义数表中的第
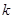行第
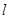列的数为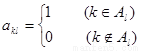
.
|
|
|
… |
|
|
|
|
… |
|
|
… |
… |
… |
… |
|
|
|
… |
|
（Ⅰ）当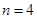
时，判断下列两个集合组是否具有性质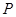，如果是请画出所对应的表格，如果不是请说明理由；
集合组1：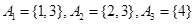
；
集合组2：
.
（Ⅱ）当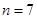
时，若集合组
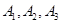具有性质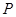，请先画出所对应的
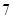行3列的一个数表，再依此表格分别写出集合；
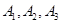（Ⅲ）当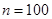
时，集合组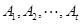
是具有性质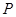且所含集合个数最小的集合组，求
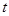的值及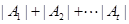
的最小值.（其中
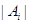表示集合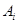
所含元素的个数）
查看答案和解析>>
科目：高中数学 来源： 题型：
若
为集合
且
的子集，且满足两个条件：
①
；
②对任意的
，至少存在一个
，使
或
.
|
|
| … |
|
|
|
| … |
|
| … | … | … | … |
|
|
| … |
|
则称集合组具有性质
.
如图，作
行
列数表，定义数表中的第
行第
列的数为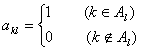
.
（Ⅰ）当
时，判断下列两个集合组是否具有性质，如果是请画出所对应的表格，如果不是请说明理由；
集合组1：
；
集合组2：
.
（Ⅱ）当
时，若集合组
具有性质，请先画出所对应的
行3列的一个数表，再依此表格分别写出集合；
（Ⅲ）当
时，集合组
是具有性质且所含集合个数最小的集合组，求
的值及
的最小值.（其中
表示集合
所含元素的个数）
查看答案和解析>>
科目：高中数学 来源： 题型：
（本小题满分13分）
若
为集合
且
的子集，且满足两个条件：
①
；
②对任意的
，至少存在一个
，使
或
.
|
|
| … |
|
|
|
| … |
|
| … | … | … | … |
|
|
| … |
|
则称集合组具有性质
.
如图，作
行
列数表，定义数表中的第
行第
列的数为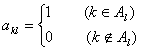
.
（Ⅰ）当
时，判断下列两个集合组是否具有性质，如果是请画出所对应的表格，如果不是请说明理由；
集合组1：
；
集合组2：
.
（Ⅱ）当
时，若集合组
具有性质，请先画出所对应的
行3列的一个数表，再依此表格分别写出集合；
（Ⅲ）当
时，集合组
是具有性质且所含集合个数最小的集合组，求
的值及
的最小值.（其中
表示集合
所含元素的个数）
查看答案和解析>>
科目：高中数学 来源：2011届北京市西城区高三二模考试理科数学 题型：解答题
（（本小题满分13分）
若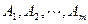
为集合
且
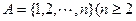的子集，且满足两个条件：
①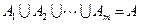
；
②对任意的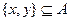
，至少存在一个
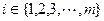，使
或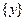
.
则称集合组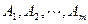具有性质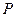
.
如图，作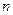
行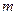
列数表，定义数表中的第
行第
列的数为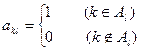
.
 |  | … |  |
 |  | … |  |
| … | … | … | … |
 |  | … |  |
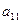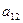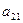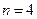时，判断下列两个集合组是否具有性质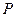，如果是请画出所对应的表格，如果不是请说明理由；
；
.
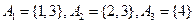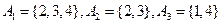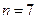时，若集合组
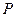具有性质，请先画出所对应的
行3列的一个数表，再依此表格分别写出集合；
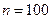时，集合组
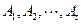是具有性质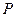且所含集合个数最小的集合组，求
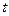的值及
的最小值.（其中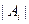
表示集合
所含元素的个数）查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，集合
，则
______.
