
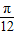 个单位长度
个单位长度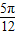 个单位长度
个单位长度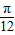 个单位长度
个单位长度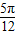 个单位长度
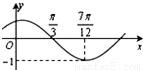
个单位长度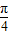 ,则周期T=π,求得ω=2,运用五点作图原理求得Φ,求出f(x)后,即可验证排除,也可运用诱导公式尝试.
,则周期T=π,求得ω=2,运用五点作图原理求得Φ,求出f(x)后,即可验证排除,也可运用诱导公式尝试.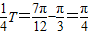 ,所以T=π,所以ω=2,再由
,所以T=π,所以ω=2,再由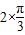 +Φ=π,得Φ=
+Φ=π,得Φ=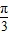 ,所以f(x)=sin(2x+
,所以f(x)=sin(2x+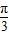 ),要得到g(x)=-Acosωx=-cos2x的图象,把f(x)=sin(2x+
),要得到g(x)=-Acosωx=-cos2x的图象,把f(x)=sin(2x+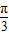 )中的x变为x-
)中的x变为x-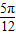 ,即f(x-
,即f(x-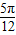 )=sin[2(x-
)=sin[2(x-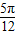 )+
)+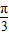 ]=sin(2x-
]=sin(2x-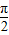 )=-cos2x.所以只要将f(x)=sin(2x+
)=-cos2x.所以只要将f(x)=sin(2x+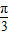 )向右平移
)向右平移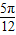 个单位长度就能得到g(x)的图象.
个单位长度就能得到g(x)的图象.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
| a |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 函数f(x)=Asin(ωx+?)(其中A>0,ω>0,|?|<
函数f(x)=Asin(ωx+?)(其中A>0,ω>0,|?|<| π |
| 2 |
| π |
| 12 |
| π |
| 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 4 |
| 2π |
| 3 |
| π |
| 2 |
| 2 |
| 3 |
| π |
| 12 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
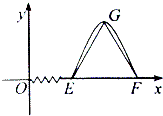 已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是边长为2的正三角形,则f(1)=( )
已知函数f(x)=Asinωx(A>0,ω>0)的部分图象如图所示,若△EFG是边长为2的正三角形,则f(1)=( )A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com