
思路分析:我们知道等差、等比数列的通项公式都是通过递推得出结论的,无法用演绎法证明它们的无穷性,数学归纳法以一次逻辑的推理代替了无限的验证过程.
证明:(1)当n=1时,左=a1,
右=a1+(1-1)d=a1,所以等式成立.
(2)假设当n=k(k∈N)时等式成立,即ak=a1+(k-1)d.
那么ak+1=ak+d=a1+(k-1)d+d=a1+[(k+1)-1]d.
∴当n=k+1时,等式成立,由(1)(2)知对任何n∈N*等式成立.
方法归纳
因为数列的通项公式,前n项和公式都是关于自然数n的函数,所以在关于这类问题的证明上,如果我们无法确定其他比较简便的证明方法,那么数学归纳法是证明它们的一种有效方法.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
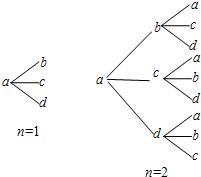 用a,b,c,d四个不同字母组成一个含n+1(n∈N+)个字母的字符串,要求由a开始,相邻两个字母不同.例如n=1时,排出的字符串是ab,ac,ad;n=2时排出的字符串是aba,abc,abd,aca,acb,acd,ada,adb,adc,…,如图所示.记这含n+1个字母的所有字符串中,排在最后一个的字母仍是a的字符串的种数为an.
用a,b,c,d四个不同字母组成一个含n+1(n∈N+)个字母的字符串,要求由a开始,相邻两个字母不同.例如n=1时,排出的字符串是ab,ac,ad;n=2时排出的字符串是aba,abc,abd,aca,acb,acd,ada,adb,adc,…,如图所示.记这含n+1个字母的所有字符串中,排在最后一个的字母仍是a的字符串的种数为an.| 3n+3(-1)n |
| 4 |
| 2 |
| 9 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2n |
|
| 2m-1 |
| 2n |
查看答案和解析>>
科目:高中数学 来源: 题型:
用![]() 四个不同字母组成一个含
四个不同字母组成一个含![]()
![]() 个字母的字符串,要求由
个字母的字符串,要求由![]() 开始,相邻两个字母不同. 例如
开始,相邻两个字母不同. 例如![]() 时,排出的字符串是
时,排出的字符串是![]() ;
;![]() 时排出的字符串是
时排出的字符串是![]() ,……, 如图所示.记这含
,……, 如图所示.记这含![]() 个字母的所有字符串中,排在最后一个的字母仍是
个字母的所有字符串中,排在最后一个的字母仍是![]() 的字符串的种数为
的字符串的种数为![]() .
.
(1)试用数学归纳法证明:![]() ;
;
(2)现从![]() 四个字母组成的含
四个字母组成的含![]() 个字母的所有字符串中随机抽取一个字符串,字符串最后一个的字母恰好是
个字母的所有字符串中随机抽取一个字符串,字符串最后一个的字母恰好是![]() 的概率为
的概率为![]() ,求证:
,求证:![]() .
.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省海安高级中学、南京外国语学校、金陵中学高三调研数学试卷(解析版) 题型:解答题
 ;
; .
.
查看答案和解析>>
科目:高中数学 来源:2010年江苏省连云港市东海高级中学高考数学考前猜题试卷(2)(解析版) 题型:解答题
 ;
; .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com