
 ,对于n∈N*,定义fn+1(x)=f1[fn(x)],则f2011(x)=________.
,对于n∈N*,定义fn+1(x)=f1[fn(x)],则f2011(x)=________.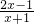
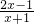 )=
)= .f3(x)=f1(
.f3(x)=f1( )=
)= ,f4(x)=f1(
,f4(x)=f1( )=
)= ,f5(x)=f1(
,f5(x)=f1( )=
)= ,f6(x)=f1(
,f6(x)=f1( )=x,f7(x)=f1(x)=
)=x,f7(x)=f1(x)=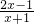 .所以从f1(x)到f6(x),每6个一循环.由此能求出结果.
.所以从f1(x)到f6(x),每6个一循环.由此能求出结果.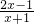 )=
)= =
= .
. )=
)= =
= ,
, )=
)= =
= ,
, )=
)= =
= ,
, )=
)= =x,
=x,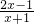 =f1(x).
=f1(x). ,
,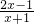 .
.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| n |
 |
| i=1 |
| 2Sn |
| an |
| (n+anbn)2+7-2n |
| n |
| m |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 4x |
| 4x+2 |
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省南通市海门中学高二(下)期中数学试卷(理科)(解析版) 题型:填空题
 ,对于n∈N*,定义fn+1(x)=f1[fn(x)],则f2011(x)= .
,对于n∈N*,定义fn+1(x)=f1[fn(x)],则f2011(x)= .查看答案和解析>>
科目:高中数学 来源:2009年浙江省温州市摇篮杯高一数学竞赛试卷(解析版) 题型:解答题
 ,对于n∈N+,定义f1(x)=f(x),fn+1(x)=f[fn(x)],偶函数g(x)的定义域为{x|x≠0},
,对于n∈N+,定义f1(x)=f(x),fn+1(x)=f[fn(x)],偶函数g(x)的定义域为{x|x≠0},查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com