在数列{an}中,若an2-an-12=p(n≥2,n∈N*,p为常数),则{an}称为“等方差数列”,下列是对“等方差数列”的判断:
①若{an}为等方差数列,则{an2}是等差数列;
②{(-1)n}是等方差数列;
③若{an}是等方差数列,则{akn}(k∈N*,k为常数)也是等方差数列.
其中正确命题序号为 .
【答案】
分析:根据“等方差数列”的定义,数列{a
n}中,若
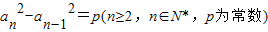
,则{a
n}称为“等方差数列”,我们逐一判断①②③中的三个数列是否满足等方差数列的定义,可得答案.
解答:解:①∵{a
n}是等方差数列,
∴a
n2-a
n-12=p(p为常数)
∴{a
n2}是等差数列,故①正确;
②数列{(-1)
n}中,a
n2-a
n-12=[(-1)
n]
2-[(-1)
n-1]
2=0,
∴{(-1)
n}是等方差数列;故②正确;
③数列{a
n}中的项列举出来是,a
1,a
2,…,a
k,…,a
2k,…
数列{a
kn}中的项列举出来是,a
k,a
2k,…,a
3k,…,
∵(a
k+12-a
k2)=(a
k+22-a
k+12)=(a
k+32-a
k+22)=…=(a
2k2-a
2k-12)=p
∴(a
k+12-a
k2)+(a
k+22-a
k+12)+(a
k+32-a
k+22)+…+(a
2k2-a
2k-12)=kp
∴(a
kn+12-a
kn2)=kp
∴{a
kn}(k∈N
*,k为常数)是等方差数列;故③正确;
故答案为:①②③
点评:本题考查等差数列的定义及其应用,解题时要注意掌握数列的概念,属基础题.

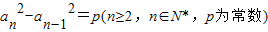 ,则{an}称为“等方差数列”,我们逐一判断①②③中的三个数列是否满足等方差数列的定义,可得答案.
,则{an}称为“等方差数列”,我们逐一判断①②③中的三个数列是否满足等方差数列的定义,可得答案.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案