
(Ⅰ)写出明年第x个月的需求量g(x)(万件)与月x的函数关系,并求出哪个月份的需求量最大,最大需求量是多少?
(Ⅱ)如果将该商品每月都投放市场p万件(销售未完的商品都可以在以后各月销售),要保证每月都足量供应,问:p至少为多少万件?
答案:(Ⅰ)g(1)=f(1)=![]() ·1·(1+1)·(35-2)=
·1·(1+1)·(35-2)=![]() .
.
当x≥2时,
g(x)=f(x)-f(x-1)
=![]() x(x-1)(35-2x)-
x(x-1)(35-2x)-![]() (x-1/x(37-2x)
(x-1/x(37-2x)
=![]() x·[(35+33x-2x2)-(-37+39x-2x2)]
x·[(35+33x-2x2)-(-37+39x-2x2)]
=![]() x·(72-6x)=
x·(72-6x)=![]() x·(12-x).
x·(12-x).
∴g(x)=![]() x(12-x)(x∈N*,且x≤12).
x(12-x)(x∈N*,且x≤12).
∵g(x)≤![]()
![]() .
.
∴当x=12-x,即x=6时,g(x)max=![]() (万件).
(万件).
故6月份该商品的需求量最大,最大需求量为![]() 万件.
万件.
(Ⅱ)依题意,对一切x∈{1,2,…,12}有
px≥g(1)+g(2)+…+g(x)=f(x)。
∴p≥![]() (x+1)(35-2x)(x=1,2,…,12).
(x+1)(35-2x)(x=1,2,…,12).
∵h(x)= ![]() (35+33x-2x2)=
(35+33x-2x2)=![]()
∴h(x)max=h(8)=1.14.故p≥1.14.故每个月至少投放1.14万件,可以保证每个月都保证供应.


科目:高中数学 来源: 题型:
| 1 | 150 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 150 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 150 |
查看答案和解析>>
科目:高中数学 来源:2011年高三数学第一轮基础知识训练(26)(解析版) 题型:解答题
 x(x+1)(35-2x)(x∈N*,且x≤12).
x(x+1)(35-2x)(x∈N*,且x≤12).查看答案和解析>>
科目:高中数学 来源:2012届福建省四地六校联考上学期高三第三次月考理科数学试卷 题型:解答题
某地区预计明年从年初开始的前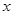 个月内,对某种商品的需求总量
个月内,对某种商品的需求总量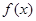 (万件)与月份
(万件)与月份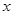 的近似关系为
的近似关系为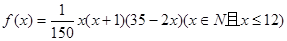 .
.
(1)写出明年第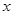 个月的需求量
个月的需求量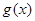 (万件)与月份
(万件)与月份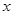 的函数关系式,并求出哪个月份的需求量超过1.4万件;
的函数关系式,并求出哪个月份的需求量超过1.4万件;
(2)如果将该商品每月都投放市场p万件,要保持每月都满足市场需求,则p至少为多少万件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com