
分析 (1)根据基本不等式即可证明,
(2)根据对数的性质求出log2a+log2b=1,根据基本不等式即可求出.
解答 解:(1)证明:由$a+2b=\frac{4}{a}+\frac{2}{b}$(a>0,b>0)得,$a+2b=\frac{2a+4b}{a•b}$,即ab=2,
∴$a+2b≥2\sqrt{a•2b}=2\sqrt{4}=4$,当且仅当a=2b=2时取等号.
(2)∵log2a+log2b=log2(ab)=log22=1,
∴$\frac{1}{{{{log}_2}a}}+\frac{3}{{{{log}_2}b}}=(\frac{1}{{{{log}_2}a}}+\frac{3}{{{{log}_2}b}})•({log_2}a+{log_2}b)=4+\frac{{{{log}_2}b}}{{{{log}_2}a}}+\frac{{3{{log}_2}a}}{{{{log}_2}b}}$,
∵(a-1)(b-1)>0,
∴0<a<1,0<b<1或a>1,b>1,
则$\frac{{{{log}_2}b}}{{{{log}_2}a}}>0,\frac{{3{{log}_2}a}}{{{{log}_2}b}}>0$,
∴$4+\frac{{{{log}_2}b}}{{{{log}_2}a}}+\frac{{3{{log}_2}a}}{{{{log}_2}b}}≥4+2\sqrt{3}$,
即$\frac{1}{{{{log}_2}a}}+\frac{3}{{{{log}_2}b}}$的最小值为$4+2\sqrt{3}$.
点评 本题考查了基本不等式的应用,关键是掌握不等式成立的条件,属于基础题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$$\overrightarrow{DA}$ | B. | $\frac{1}{3}$$\overrightarrow{DA}$ | C. | $\frac{1}{4}$$\overrightarrow{DA}$ | D. | $\overrightarrow{0}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-4,5] | B. | [-5,5] | C. | [4,5] | D. | [-5,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
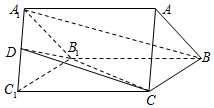 如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,BC=CC1,D是A1C1中点.
如图,在三棱柱ABC-A1B1C1中,△ABC是等边三角形,BC=CC1,D是A1C1中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 21 | C. | 3 | D. | -21 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (-1,0) | C. | (-2,-1)∪(-1,0) | D. | (-2,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com