
已知抛物线![]() 过焦点
过焦点![]() 的任一条弦
的任一条弦![]() ,设
,设![]() 且
且![]()

(1)若![]() ,求抛物线方程;
,求抛物线方程;
(2)是否存在常数![]() ,使
,使![]() ,若存在,求出
,若存在,求出![]() 的值,并给予证明,若不存在,请说明理由;
的值,并给予证明,若不存在,请说明理由;
(3)在抛物线对称轴(![]() 的正方向)上是否存在一定点
的正方向)上是否存在一定点![]() ,经过点
,经过点![]() 的任意一条弦
的任意一条弦![]() ,使
,使![]() 为定值,若存在,则求出定点
为定值,若存在,则求出定点![]() 的坐标和定值,若不存在,请说明理由.
的坐标和定值,若不存在,请说明理由.
(1)![]() (2)存在,
(2)存在,![]() (3)存在,定点为
(3)存在,定点为![]() ,定值为
,定值为![]()
(1)解:设![]() 代入
代入![]()
得![]()
所以,抛物线方程为![]() -----------------------------------------------------------------------4分
-----------------------------------------------------------------------4分
(2)![]() 当
当![]() 轴时,
轴时,![]()
猜想:存在![]()
![]() 一般地证明:
一般地证明:![]() ,其中
,其中![]() 是
是![]() 的斜率,由抛物线的定义知
的斜率,由抛物线的定义知![]() ,同理
,同理![]()
![]() ,证毕-------10分
,证毕-------10分
(3)解:假设存在这样的定点![]()
![]() 先探求定点坐标及定值,当
先探求定点坐标及定值,当![]() 轴时,有
轴时,有![]() ,又
,又![]()
![]() ,当
,当![]() 绕点
绕点![]() 转动时,点
转动时,点![]() 点,
点,
得![]() ,点
,点![]() 无穷远,
无穷远,![]() ,
,![]() ,由假设知
,由假设知
![]() ,猜想过定点为
,猜想过定点为![]() ,定值为
,定值为![]() ---------------------------------13分
---------------------------------13分
![]() 再证明:结论:存在定点
再证明:结论:存在定点![]() ,过
,过![]() 点的任意弦
点的任意弦![]() ,使
,使![]() (定值)设
(定值)设![]() ,代入
,代入![]() ,得
,得![]() ,记
,记![]() ,
,
则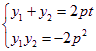 ,而
,而![]() ,
,
![]() ,
,
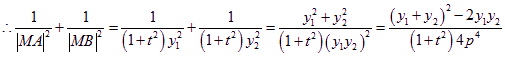
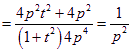 (定值)------------------------------------------------------------------------18分
(定值)------------------------------------------------------------------------18分


科目:高中数学 来源: 题型:
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知抛物线x2=4y的焦点为F,过F任作直线l(l与x轴不平行)交抛物线分别于A,B两点,点A关于y轴对称点为C,
已知抛物线x2=4y的焦点为F,过F任作直线l(l与x轴不平行)交抛物线分别于A,B两点,点A关于y轴对称点为C,| |AB| |
| |DE| |
| |AB| |
| |DE| |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010-2011学年黑龙江省等四校高三第一次模拟考试数学理卷 题型:选择题
已知抛物线 ,
, 为其焦点,
为其焦点, 为其准线,过
为其准线,过 任作一条直线交抛物线于
任作一条直线交抛物线于 、
、 两点,
两点, 、
、 分别为
分别为 、
、 在
在 上的射影,
上的射影, 为
为 的中点,给出下列命题:
的中点,给出下列命题:
① ;
;
② ;
;
③ ∥
∥ ;
;
④ 与
与 的交点在
的交点在 轴上;
轴上;
⑤ 与
与 交于原点.
交于原点.
其中真命题的个数为
A. 个 B.
个 B. 个 C.
个 C. 个 D.
个 D. 个
个
查看答案和解析>>
科目:高中数学 来源:2013-2014学年浙江省温州市八校联考高三(上)期初数学试卷(文科)(解析版) 题型:解答题
 的最小值,并求当
的最小值,并求当 取最小值时直线l的方程.
取最小值时直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com