已知函数f(x)=x2-x+alnx
(1)当x≥1时,f(x)≤x2恒成立,求a的取值范围;
(2)讨论f(x)在定义域上的单调性.
解:(1)由f(x)≤x
2恒成立,得:alnx≤x在x≥1时恒成立
当x=1时a∈R
当x>1时即

,令
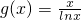
,
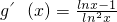
x≥e时g'(x)≥0,g(x)在x>e时为增函数,g(x)在x<e时为减函数
∴g
min(x)=e∴a≤e
(2)解:f(x)=x
2-x+alnx,f′(x)=2x-1+

=
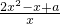
,x>0
(1)当△=1-8a≤0,a≥

时,f′(x)≥0恒成立,
f(x)在(0,+∞)上为增函数.
(2)当a<

时
①当0<a<

时,
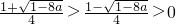
,
f(x)在
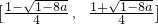
上为减函数,
f(x)在
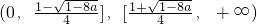
上为增函数.
②当a=0时,f(x)在(0,1]上为减函数,f(x)在[1,+∞)上为增函数
③当a<0时,
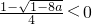
,故f(x)在(0,
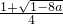
]上为减函数,
f(x)在[
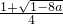
,+∞)上为增函数.
分析:(1)先利用参数分离法将a分离出来,然后研究函数的最值,使参数a恒小于函数的最小值即可;
(2)先确定函数的定义域然后求导数fˊ(x),在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,主要进行分离讨论.
点评:本题主要考查了利用导数研究函数的单调性,以及利用导数求闭区间上函数的最值,属于中档题.

 ,令
,令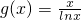 ,
,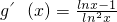
 =
=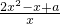 ,x>0
,x>0 时,f′(x)≥0恒成立,
时,f′(x)≥0恒成立, 时
时 时,
时,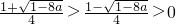 ,
,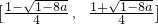 上为减函数,
上为减函数,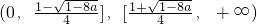 上为增函数.
上为增函数.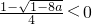 ,故f(x)在(0,
,故f(x)在(0,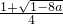 ]上为减函数,
]上为减函数,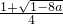 ,+∞)上为增函数.
,+∞)上为增函数.

 阅读快车系列答案
阅读快车系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<