

分析 (1)在Rt△DEF中,由已知可得∠DEF=45°,在Rt△ABE中,得到∠AEB=45°,则可得到EF⊥BE,结合平面PBE⊥平面BCDE,可得EF⊥平面PBE,从而得到平面PBE⊥平面PEF;
(2)过P做PO⊥BE,由面面垂直的性质及线面垂直的判定得到PO⊥平面BCDE,即PO为四棱锥P-BCFE的高.把S四边形BCFE转化为S矩形ABCD-S△ABE-S△DEF,求值后代入棱锥的体积公式得答案.
解答 (1)证明:如图,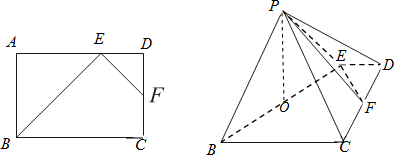 在Rt△DEF中,∵ED=DF,∴∠DEF=45°.
在Rt△DEF中,∵ED=DF,∴∠DEF=45°.
在Rt△ABE中,∵AE=AB,∴∠AEB=45°,
∴∠BEF=90°,则EF⊥BE.
∵平面PBE⊥平面BCDE,且平面PBE∩平面BCDE=BE,
∴EF⊥平面PBE,
∵EF?平面PEF,∴平面PBE⊥平面PEF;
(2)解:过P做PO⊥BE,
∵PO?平面PBE,平面PBE⊥平面BCDE且平面PBE∩平面BCDE=BE,
∴PO⊥平面BCDE,
四棱锥P-BCFE的高h=PO=$2\sqrt{2}$.
S四边形BCFE=S矩形ABCD-S△ABE$-{S}_{△DEF}=6×4-\frac{1}{2}×4×4-\frac{1}{2}×2×2=14$,
则${V}_{P-BCFE}=\frac{1}{3}{S}_{四边形BCFE}•h$=$\frac{1}{3}×14×2\sqrt{2}=\frac{28\sqrt{2}}{3}$.
点评 本题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力,是中档题.


科目:高中数学 来源: 题型:解答题
| X | 0 | 1 |
| P | 0.5 | 0.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
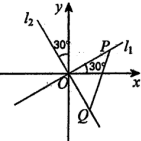 如图,两条过原点.D的直线l1,l2分别与x轴、y轴正方向成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.
如图,两条过原点.D的直线l1,l2分别与x轴、y轴正方向成30°的角,点P(x1,y1)在直线l1上运动,点Q(x2,y2)在直线l2上运动,且线段PQ的长度为2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n2 | B. | n2+n | C. | 2n-1 | D. | 2n+1-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
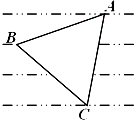 如图所示,某服装设计师要在一块条形布料上画一个等边△ABC作为点缀,使A、B、C三点分别落在条形布料的线条上,已知条形布料相邻横线间的距离为3厘米,则等边△ABC的边长应为2$\sqrt{21}$厘米.
如图所示,某服装设计师要在一块条形布料上画一个等边△ABC作为点缀,使A、B、C三点分别落在条形布料的线条上,已知条形布料相邻横线间的距离为3厘米,则等边△ABC的边长应为2$\sqrt{21}$厘米.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com