练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知如右图，边长为a的菱形ABCD中，∠ABC=60°，PC⊥平面ABCD，E是PA的中点，求E到平面PBC的距离．

    答案：
    解析：

    解法一：注意到点E在PA上，可将E到平面PBC的距离转化为A到平面PBC的距离的一半．由PC⊥平面ABCD，有平面PBC⊥平面ABCD，故过A在平面ABCD内作AH⊥BC，交BC于H，则AH=．于是，所求距离为．

    解法二：将E到平面PBC的距离转化为线面距离，再转化为点面距离．连结AC、BD，设AC交BD于O，则EO∥平面PBC，于是直线OE上任意一点到平面PBC的距离都相等，由平面PBC⊥平面ABCD．若过O作OG⊥平面PBC，则垂足必在BC上，故线段OG即为所求．

       ∵∠ACB=60°，AC=BC=AB=a，

    ∴OC=a，OG=OC·sin60°=．

    ∴O到平面PBC的距离为，即E到平面PBC的距离为


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

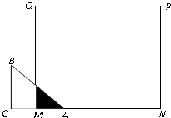    已知如图，等腰三角形ABC的直角边长为a，正方形MNPQ的边为b （a＜b），C、M、A、N在同一条直线上，开始时点A与点M重合，让△ABC向右移动，最后点C与点N重合．设三角形与正方形的重合面积为y，点A移动的距离为x，则y关于x的大致图象是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，已知椭圆M：
    y2
    a2
    +
    x2
    b2
    =1    （a＞b＞0）的四个顶点构成边长为5的菱形，原点O到直线AB的距离为
    12
    5
    ，其A（0，a），B（-b，0）．直线l：x=my+n与椭圆M相交于C，D两点，且以CD为直径的圆过椭圆的右顶点P（其中点C，D与点P不重合）．
    （1）求椭圆M的方程；
    （2）试判断直线l与x轴是否交于定点？若是，求出定点的坐标；若不是，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：044

    已知如右图，边长为a的菱形ABCD中，∠ABC=60°，PC⊥平面ABCD，E是PA的中点，求E到平面PBC的距离．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年重庆94中高三（上）第五次月考数学试卷（解析版） 题型：选择题

    已知如图，等腰三角形ABC的直角边长为a，正方形MNPQ的边为b （a＜b），C、M、A、N在同一条直线上，开始时点A与点M重合，让△ABC向右移动，最后点C与点N重合．设三角形与正方形的重合面积为y，点A移动的距离为x，则y关于x的大致图象是（ ）

    A．
    B．
    C．
    D．

    查看答案和解析>>

    同步练习册答案