练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知10α＝2，10β＝3，则100＝________．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：设计必修一数学北师版 北师版 题型：022

    已知10α＝2，10β＝3，则＝________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知二次函数f(x)＝ax2＋bx＋c(x∈R)的部分对应值如表.

    x

    －3

    －2

    －1

    0

    1

    2

    3

    4

    5

    …

    y

    －24

    －10

    0

    6

    8

    6

    0

    －10

    －24

    …

    则使ax2＋bx＋c＞0成立的x的取值范围是(　　)

    A．(－10，－1)∪(1＋∞)

    B．(－∞，－1)∪(3＋∞)

    C．(－1,3)

    D．(0，＋∞)

    查看答案和解析>>

    科目：高中数学 来源：2011年福建省罗源县第一中学高二上学期期中考试文科数学 题型：解答题

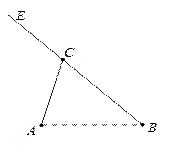
    （本小题满分12分） 如图，A，B，C是三个汽车站，AC，BE是直线型公路．已知AB＝120 km，∠BAC＝75°，∠ABC＝45°．有一辆车（称甲车）以每小时96（km）的速度往返于车站A，C之间，到达车站后停留10分钟；另有一辆车（称乙车）以每小时120（km）的速度从车站B开往另一个城市E，途经车站C，并在车站C也停留10分钟．已知早上8点时甲车从车站A、乙车从车站B同时开出．
    （1）计算A，C两站距离，及B，C两站距离；（2）若甲、乙两车上各有一名旅客需要交换到对方汽车上，问能否在车站C处利用停留时间交换．（3）求10点时甲、乙两车的距离．（可能用到的参考数据：，，，）

    查看答案和解析>>

    科目：高中数学 来源：2014届山东省高一第二学期期中考试数学试卷（解析版） 题型：解答题

    已知sina＝,aÎ(,p)，cosb＝－，b是第三象限的角.

    ⑴ 求cos(a－b)的值；

    ⑵ 求sin(a＋b)的值；

    ⑶ 求tan2a的值.

    【解析】第一问中∵ aÎ(,p),∴ cosa＝－＝－,  ∵ b是第三象限的角，

    ∴ sinb＝－＝－,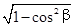     

    cos(a－b)＝cosa·cosb＋sina·sinb ＝(－)×(－)＋×(－)＝－ 

    ⑵ 中sin(a＋b)＝sina·cosb＋cosa·sinb       ＝×(－)＋(－)×(－)＝ ⑶ 利用二倍角的正切公式得到。∵tana＝＝－ ∴tan2a＝ ＝＝－ 

    解∵ aÎ(,p),∴ cosa＝－＝－,         …………1分

    ∵ b是第三象限的角，∴ sinb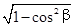＝－＝－,        ………2分

    ⑴ cos(a－b)＝cosa·cosb＋sina·sinb          …………3分

    ＝(－)×(－)＋×(－)＝－          ………………5分

    ⑵ sin(a＋b)＝sina·cosb＋cosa·sinb          ……………………6分

    ＝×(－)＋(－)×(－)＝           …………………8分

    ⑶ ∵tana＝＝－             …………………9分

    ∴tan2a＝             ………………10分

    ＝＝－

     

    查看答案和解析>>

    同步练习册答案