
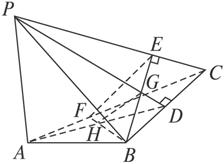
图2-3-4
思路分析:欲证HG⊥平面PBC,需证HG与平面PBC内的两条相交直线垂直.利用“垂心和三角形顶点的连线垂直于对边”的性质,可使孤立的点G、H与各边联系起来,并得到垂直关系,从而找到解题突破口.首先连结AH,并延长交BC于点D,连结PD,则根据线面垂直及已知条件得PD⊥BC,AD⊥BC,从而BC⊥平面PAD,且BC⊥HG.再连结并延长BG、BH分别交对边于E、F,则PC⊥BE且BF⊥AC,从而PC⊥BF,推出PC⊥平面BEF,PC⊥HG.
证明:连结AH并延长交BC于D,连结PD.
H为△ABC的垂心![]() AD⊥BC.
AD⊥BC.
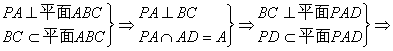
BC⊥PD![]() G∈PD且HC⊥BC.
G∈PD且HC⊥BC.
连结并延长BG、BH分别交PC、AC于点E、F,连结EF.
H为△ABC的垂心,?
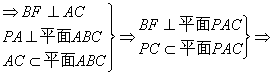
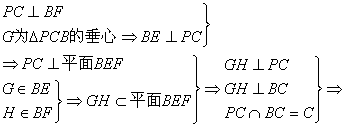 GH⊥平面PBC.
GH⊥平面PBC.
绿色通道:解决立体几何中的有关垂直关系的问题,常常要进行多次线线垂直和线面垂直之间的转化,这充分体现了数学化归思想的重要性和优越性.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
 (2012•宝鸡模拟)如图,已知PA⊥平面ABC,且PA=
(2012•宝鸡模拟)如图,已知PA⊥平面ABC,且PA=| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D,E分别是BC,AP的中点.
(2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D,E分别是BC,AP的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D是AB的中点.
(2012•徐汇区一模)如图,已知PA⊥平面ABC,AC⊥AB,AP=BC=2,∠CBA=30°,D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•盐城三模)如图,三棱锥P-ABC中,已知PA⊥平面ABC,△ABC是边长为2的正三角形,D,E分别为PB,PC中点.
(2013•盐城三模)如图,三棱锥P-ABC中,已知PA⊥平面ABC,△ABC是边长为2的正三角形,D,E分别为PB,PC中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com