
已知函数
 .
.
(1)
求证f(x)在(1,+∞)上为增函数.(2)
若a=3,求方程f(x)=0的正根(精确到0.01)|
(1) 任取 , , ,且 ,且 , ,
则  , , ,且 ,且 ,∴ ,∴ . .
又∵  , , ,∴ ,∴ . .
于是  . .
故函数 f(x)在(-1,+∞)上为增函数.(2) 由(1)知,当a=3时, 也在(-1,+∞)上为增函数,故在(0,+∞)也单调递增,因此f(x)=0的正根仅有一个,以下用二分法求这一正根. 也在(-1,+∞)上为增函数,故在(0,+∞)也单调递增,因此f(x)=0的正根仅有一个,以下用二分法求这一正根.
由于 f(0)=-1<0, ,取[0,1]为初始区间,用二分法逐次计算.列出下表: ,取[0,1]为初始区间,用二分法逐次计算.列出下表:
由于区间 [0.27343,0.28125]的长度为0.00782<0.01,所以这一区间的两个端点的近似值0.28就是方程的根的近似值,即原方程的正根是0.28.用二分法求函数零点的近似值  ,要精确度为ε,即零点的近似值 ,要精确度为ε,即零点的近似值 与零点的真值α的误差不超过ε,零点近似值 与零点的真值α的误差不超过ε,零点近似值 的选取有以下方法: 的选取有以下方法:
(1) 若区间(a,b)使|a-b|<ε,则因零点值α (a,b),∴a(或b)与真值α满足|a-α|<ε或|b-α|<ε,所以只需取零点近似值 (a,b),∴a(或b)与真值α满足|a-α|<ε或|b-α|<ε,所以只需取零点近似值 . .
(2) 在区间 使 使 ,取零点近似值 ,取零点近似值 ,则 ,则 . . |


科目:高中数学 来源:2013-2014学年山东省济南市高三上学期期末考试理科数学试卷(解析版) 题型:解答题
已知函数 .
.
(1)求 的单调区间;
的单调区间;
(2)若 ,
, 在区间
在区间 恒成立,求a的取值范围.
恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届山东省济宁市高二5月质量检测理科数学试卷(解析版) 题型:解答题
已知函数 .
.
(1)求 的单调区间;
的单调区间;
(2)当 时,判断
时,判断 和
和 的大小,并说明理由;
的大小,并说明理由;
(3)求证:当 时,关于
时,关于 的方程:
的方程: 在区间
在区间 上总有两个不同的解.
上总有两个不同的解.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省汕头市高三毕业班教学质量检测文科数学(含解析) 题型:解答题
(本题满分14分)
已知函数 ,
,
(1)求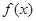 的最小值;
的最小值;
(2)若对所有 都有
都有 ,求实数
,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com