
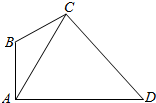
 在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.
在如图所示的四边形ABCD中,已知AB⊥AD,∠ABC=120°,∠ACD=60°,AD=2$\sqrt{3}$,设∠ACB=θ,点C到AD的距离为h.分析 (1)在△ACD中使用正弦定理求出CD,则h=CDsin∠ADC;
(2)在△ACD中使用正弦定理求出AC,在△ABC中使用正弦定理用θ表示出AB,BC,将问题转化为三角函数的最值问题求解;
(3)△ABD的外接圆与△CBD的外接圆重合可知四点共圆,从而求出∠ACB和∠BAC,使用正弦定理解出各边,带入面积公式.
解答 解:(1)∠BAC=180°-120°-15°=45°,∠CAD=90°-∠BAC=45°,∴∠ADC=75°.
在△ACD中,由正弦定理得:$\frac{AD}{sin60°}=\frac{CD}{sin45°}$,∴CD=$\frac{ADsin45°}{sin60°}$=2$\sqrt{2}$.
∴h=CD•sin∠ADC=2$\sqrt{2}$•sin75°=$\sqrt{3}$+1.
(2)∠BAC=60°-θ,∴∠CAD=30°+θ,∠ADC=90°-θ.
在△ACD中,∵$\frac{AD}{sin∠ACD}=\frac{AC}{sin∠ADC}$,∴$\frac{2\sqrt{3}}{sin60°}=\frac{AC}{sin(90°-θ)}$,解得AC=4cosθ.
在△ABC中,∵$\frac{AB}{sin∠ACB}=\frac{BC}{sin∠BAC}=\frac{AC}{sin∠ABC}$,∴$\frac{AB}{sinθ}=\frac{BC}{sin(60°-θ)}=\frac{4cosθ}{sin120°}$.
解得AB=$\frac{8sinθcosθ}{\sqrt{3}}$,BC=4cos2θ-$\frac{4sinθcosθ}{\sqrt{3}}$,
∴AB+BC=4cos2θ+$\frac{4sinθcosθ}{\sqrt{3}}$=2cos2θ+$\frac{2\sqrt{3}}{3}$sin2θ+2=$\frac{4\sqrt{3}}{3}$sin(2θ+φ)+2.
∴当sin(2θ+φ)=1时,AB+BC取得最大值$\frac{4\sqrt{3}}{3}$+2.
(3)∵△ABD的外接圆与△CBD的外接圆重合,∴A,B,C,D四点共圆.
∴∠BCD=90°,∠ACB=∠BAC=∠D=30°,
在△ABC中,∵$\frac{AC}{sin120°}=\frac{AB}{sin30°}=\frac{BC}{sin30°}$,∴AB=BC=2,∴S△ABC=$\frac{1}{2}AB•BC•sin120°$=$\sqrt{3}$.
点评 本题考查了正弦定理在解三角形中的应用,属于中档题.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A?B | B. | A=B | C. | A∩B=B | D. | A∪B=(0,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com